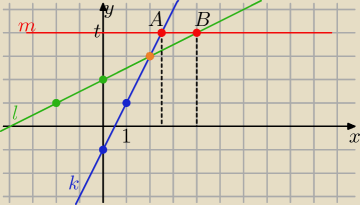
funkcja liniowa akante: proste k i l określone są równaniami y=2x−1 i y=0.5x+2 Prosta y =t przecina k i l odpowiednio w punktach A I B Długość odcinka AB wyraź jako funkcję zmiennej t Wyznacz takie punkty A i B aby odległość odcinka AB była równa 3 jakby ktoś mógł to jakoś jasno wyjaśnić

akante: podejmie sie ktos?

Eta:

	y+1		t+1
A€ k: y= 2x−1 i A€m ⇒ xA=		} i yA= t to: A(		, t)
	2		2

l: y= 0,5x+2 ⇒ 0,5x= y−2 ⇒ x= 2y−4 B € l : y=0,5x+2 i B€ m ⇒ x_B=2t−4 i y_B= t to: B(2t−4,t)

	1
|AB|= f(t) = √(xB−xA)2+(yB−yA)2= ............. =		*|3t−9|
	2

b) |AB|=3 ⇒ |3t−9|= 6 ⇒ |t−3|=2 to już myślę,że dasz radę ..... A₁(... , ....) , A₂(..., ...) B₁(..., ....) B₂(...., ...)

Eta: Bardzo fajne zadanko Pozdrawiam .......

akante: Dziękuję wszystko sie przyda już analizuję

akante: Smaczna truskawa a zadanko ciekawe

Eta:

Beti: wg mnie tak to leci: A − pkt przecięcia prostej y = 0,5x+2 i prostej y = t, więc: 0,5x+2 = t 0,5x = t − 2 /*2 x = 2t − 4 czyli A = (2t−4; t) B − pkt przecięcia prostej y = 2x − 1 i prostej y = t, więc: 2x − 1 = t 2x = t + 1 /:2 x = 0,5t + 0,5 czyli B = (0,5t+0,5; t) |AB| = f(t) = √(0,5t + 0,5 − 2t + 4)² = √(4,5 − 1,5t)² = |4,5 − 1,5t| |AB| = 3 <=> |4,5 − 1,5t| = 3 4,5 − 1,5t = 3 lub 4,5 − 1,5t = −3 1,5t = 1,5 1,5t = 7,5 t = 1 t = 5 więc: |AB| = 3 dla A = (−2,1) i B = (1,1) lub A = (6,5) i B = (3,5)

Eta:

akante: eta to kobieta zagadka definitywnie