planimetria Alaa: Na odcinku AB o długości 20 cm obrano punkt C i zbudowano dwie figury. Wyznacz położenie punktu C tak aby suma tych figur była najmniejsza jeżeli te figury to: a) kwadrat o boku AC i kwadrat o boku BC b) kwadrat o boku AC oraz półkole o średnicy BC c) kwadrat o boku AC oraz trójkąt równoboczny o boku BC

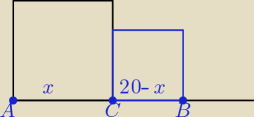
Mila: a) P_f=x²+(20−x)² i x<20 P_f=x²+400−40x+x² P_f=2x²−40x+400 Funkcja ma najmniejszą wartość w wierzchołku paraboli.

	40
xw=		=10
	4

Dla C leżącego w połowie odcinka AB b) rozwiązujesz podobnie

Alaa: tylko że w b) wychodzi mi delta ujemna i nie wiem czy dobrze rozwiązuje bo równanie układam takie (20−x)2+∏(x/2)2

Mila: A po co liczysz deltę? Masz policzyć pierwszą współrzędną wierzchołka paraboli, co Ci przeszkadza ujemna Δ. Masz obliczyć pole połowy koła.

	x
R=
	2

	1
Ppółkola=		*πR2
	2

Alaa: aha czyli podstawiam to x które wyszło mi w podpunkcie a

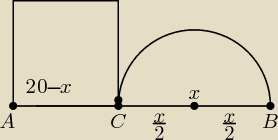
Mila: P_□=(20−x)²

	1		x		1
Po=		π*(		)2=		x2π
	2		2		8

	1
Pf=		x2π+x2−40x+400
	8

	1
Pf=(		π+1)*x2−40x+400
	8

parabola ma wartość najmniejszą w wierzchołku

	40		20
xw=		=
	2*(1/8π+1)		1/8π+1