 Poproszę o sprawdzenie:
mam funkcję i muszę określić jej przedział monotoniczność i robię to tak:
f(x)=2x5−5x4+10x2−10x+2
f'(x)=10x4−20x3+20x−10
10x4−20x3+20x−10=0 /:10
x4−2x3+2x−1=0
tabelka Hornera i wyszło mi (x−1)(x3−x2−x+1)
(x−1) x2(x−1) −1(x−1)
(x−1) (x2−1)(x−1)
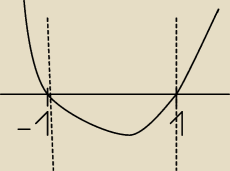
miejsca zerowe to będą: x=1, x=1, x=1, x=−1
funkcja rośnie w x∊(−∞;−1) ∪ (1:+∞)
maleje (−1;1)
max lok x= −1
min lok x = 1
Poproszę o sprawdzenie:
mam funkcję i muszę określić jej przedział monotoniczność i robię to tak:
f(x)=2x5−5x4+10x2−10x+2
f'(x)=10x4−20x3+20x−10
10x4−20x3+20x−10=0 /:10
x4−2x3+2x−1=0
tabelka Hornera i wyszło mi (x−1)(x3−x2−x+1)
(x−1) x2(x−1) −1(x−1)
(x−1) (x2−1)(x−1)
miejsca zerowe to będą: x=1, x=1, x=1, x=−1
funkcja rośnie w x∊(−∞;−1) ∪ (1:+∞)
maleje (−1;1)
max lok x= −1
min lok x = 1
| (x+5)√x−3 | ||
y= | ||
| x2−9 |