podpowie ktos marcin: Napisać równanie okręgu o środku w punkcie S(1,1), odcinającego na prostej 3x−4x+31=0 cięciwę o długości równej 16. czy tu jest blad w zapisie prostej czy ja poprostu tego nei rozumiem?

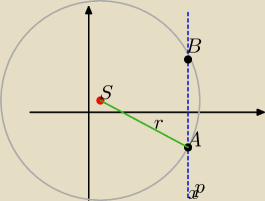
marcin: |AB|=16 prosta x=31 S(1,1) S(a,b) A(x,y) (x−a)²+(y−b)²=r² dobrze mysle?

Bogdan: Moim zdaniem jest błąd w zapisie prostej, powinno być: 3x − 4y + 31 = 0

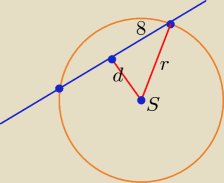
Bogdan: S = (1, 1) − środek okręgu. Równanie okręgu: (x − 1)² + (y − 1)² = r² Wystarczy najpierw wyznaczyć d, potem r. d − odległość punktu S od prostej 3x − 4y + 31 = 0.

marcin: no dzieki tak myslalem ze pewnie blad w prostej ale gdyby bylo to x=31 to dalo by sie obliczyc tylko chce wiedziec czy tym samym sposobem?

marcin: poprawiam: gdyby bylo −x + 31 = 0 to tak samo by sie liczylo? a i rownanie: (x−1)² + (y−1)² = 100