jak obliczyc ta prosta? marcin: Przez punkt A(1,2) poprowadzić prostą tworzącą z prostą x=2y kąt, którego tangens jest równy 3/2

AS:

	1
Równanie prostej danej: y =		*x
	2

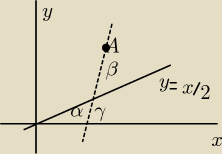
Wsp.kierunkowy tej prostej m = 1/2 , stąd mamy tgα = 1/2 Kąt β między prostymi ma być taki , by tgβ = 3/2 Kąt nachylenia szukanej prostej do osi Ox γ = α + β Wsp.kierunkowy tej prostej będzie wynosił

	tgα + tgβ
m1 = tgγ = tg(α + β) =
	1 − tgα*tgβ

Podstawiając dane mamy:

	1/2 + 3/2		2		2
m1 =		=		=		= 8
	1 − 1/2*3/2		1 − 3/4		1/4

Teraz piszę równanie prostej przez jeden punkt y − yA = m1*(x −xA) y − 2 = 8*(x − 1) y − 2 = 8*x − 8 y = 8*x − 6 Odp. Równanie szukanej prostej ma postać: y = 8*x − 6

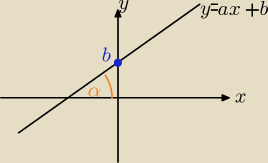
evil_woodworm: Podpowiedź: Jeżeli mamy prosta o równaniu y=ax+b, to a=tgα, a b, jest to wspołrzędna y punktu w którym prosta przecina oś y.

evil_woodworm: sorry, pomyliło mi się. znaczy to co pisałam jest ok, tylko znowu wychodzi na to, że czytac nie umiem

AS: Nic poważnego,mnie też raz po raz zdarza się zaćmienie globusa. I śpię spokojnie.

evil_woodworm: Mi ostatnio coraz częściej_. Oby minęło do października