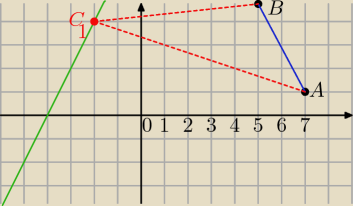
geometria analityczna madzia: Pole trójkąta ABC o wierzchołkach A=(7;1), B=(5;5) jest równe 15. a) oblicz współrzędne trzeciego wierzchołka, wiedząc że należy do prostej o równaniu 2x−y+8=0, b) napisz równanie okręgu opisanego na trójkącie ABC. zrobiłam a i C=(−2;4) lub C=(5,5;19) chce zrobić równanie do punktu C. myślałam że środek ciężkości wyznaczy a i b z tego wzoru (x₁+x₂+x₃)/2 i z y to samo ale nie to nie wychodzi proszę o pomoc

madzia: ?

madzia:

madzia: nie chce tego robić podstawiając każdy punkt np (7−a)²+(1−y)²=r² i różniej równanie

Mila: 2x−y+8=0,⇔y=2x+8 ⇔C=(x,2x+8) |AB|=√2²+4²=√20=2√5

	1
PΔ=15 i PΔ=		*2√5*h⇔√5*h=15
	2

	15
h=
	√5

	15
odległość punktu C od prostej AB wynosi
	√5

A=(7;1), B=(5;5) prosta AB: y=ax+b 1=7a+b 5=5a+b 2a=−4⇔a=−2 i 1=7*(−2)+b⇔b=15 y=−2x+15 ⇔2x+y−15=0

	|2x+2x+8−15|		15
h=		=
	√22+1		√5

Stąd |4x−7|=15 lub |4x−7|=−15

	11
x=		lub x=−2
	2

	11
y=2*		+8=19 lub y=2*(−2)+8=4
	2

	11
C=(		,19) lub C=(−2,4)
	2

2) Nie rozumiem jaki masz problem z równaniem okręgu.