narysuj wykres i omów jego własności. wajdzik: Narysuj wykres funkcji i na jego podstawie omów własności tej funkcji.

	2x+4		−2(x−3)+10		10
y=|		| =		=−2+
	3−x		x−3		x−3

Dobrze to przekształciłem?

wajdzik:

wajdzik:

Artur_z_miasta_Neptuna: intryguje mnie ... moment opuszczenia wartości bezwzględnej

wajdzik: Przepraszam, po prostu nauczyłem się tak pisać, nie wiem czemu. Wiem, że się jej tam nie opuszcza.Aczkolwiek ostatnie wyrazy są poprawne?

wajdzik:

Artur_z_miasta_Neptuna: nie 2x+4 = 2x − 6 + 10 = 2(x−3) + 10 to jest dobrze ... ale − który z mianownika wywalasz ma się dotyczyć całości a nie tylko pierwszego członu licznika ... winno być −10

wajdzik: Aaa no tak, tak to jest jak się chce zrobić wszystko w jednym działaniu. Dzięki wielki. Będę pamiętać o wartości bezwzględnej. Usuwam ją przy ostatnim działaniu tak?

wajdzik:

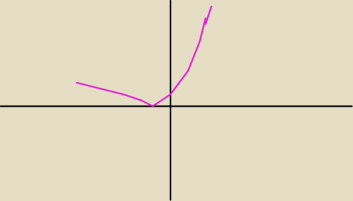
wajdzik: Coś w tym stylu mi wyszło.

wajdzik: Własności(proszę o sprawdzenie): D=x∊R\{3} Z_w=y∊<0,+∞) Funkcja nie jest okresowa Funkcja ma jedno miejsce zerowe: x₀=−2 Asymptota pionowa x=3 Asymptota pozioma y=−2 f↗, x∊<−2,3) f↘, x∊(−∞,−2> I z tego co widzę na swoim rysunku to ta funkcja JEST RÓŻNOWARTOŚCIOWA. Zgadza się wszystko?

wajdzik:

wajdzik:

Artur_z_miasta_Neptuna: asymptota poziom źle wyliczona ... y=|−2| = +2

Artur_z_miasta_Neptuna: a co się dzieje na prawo od x₀=3 tam już funkcja nie istnieje

Artur_z_miasta_Neptuna: "I z tego co widzę na swoim rysunku to ta funkcja JEST RÓŻNOWARTOŚCIOWA. Zgadza się wszystko?" Skoro funkcja jest ciągla na odcinku (a,b) ... a jednoczesnie na tym odcinku jest raz rosnąca raz malejąca ... to nie może być ona różnowartościowa (przyklad f(x) = x²)

wajdzik: Asymptotę rozumiem. Funkcję różnowartościową również. Jedno mnie jeszcze dręczy, dlaczego miejscem zerowym jest również x₀=3? Nie widzę tego.

Artur_z_miasta_Neptuna: nie jest miejscem zerowym ten punkt 'wypada' z dziedziny przecież ... natomiast w otoczeniu tego punktu dochodzi do zmiany znaku pochodnej

Artur_z_miasta_Neptuna: i może oto 'miejsce zerowe' Ci chodzi

wajdzik: "W otoczeniu tego punktu dochodzi do zmiany znaku pochodnej." Mógłbyś to rozwinąć? Pewnie coś się zmieni w tym wykresie ale nie za bardzo rozumiem jak. Nie wiem czy nie było mnie na lekcji z pochodnymi czy nie aczkolwiek myślę, że tego nie miałem lub nie brałem. Masakra

Artur_z_miasta_Neptuna: napisz jak wygląda pochodna funkcji tejże w przedziale x∊(−2,3) a jak dla x∊(3,+∞)

wajdzik: Nie brałem tego jeszcze, właśnie sprawdziłem. Ech. Co możesz poradzić jeszcze?

Artur_z_miasta_Neptuna: znak pochodnej mówi nam o MONOTONICZNOŚCI funkcji f(x) jeżeli pochodna jest ujemna (w jakimś przedziale (a,b) ) ... to w tym przedziale funkcja f(x) maleje jeżeli pochodna jest dodatnia ... to f(x) rośnie jeżeli w otoczeniu jakiegoś punktu dochodzi do zmiany znaku pochodnej i w tym punkcie x₀=0 (chyba że punkt jest poza dziedziną) to mamy tutaj ekstremum natomiast x_o=3 jest poza dziedziną ... mimo tego w rysowaniu 'szkicu' wykresu pochodnej zaznaczasz tenże punkt (ale jako niewypełniony punkt) ... aby rozwiązując metodą 'wężyka' nie zgubić rozwiązań

wajdzik: Znam metodę wężyka i to jest moja mocna strona ale nie wiem jak ją zastosować do tego. Znaczy, nie wiem które liczby wejdą na oś. Próbuję i próbuję ale nie chce mi tutaj za bardzo nic wyjść. Aczkolwiek coś już łapę

wajdzik: Artur, przepraszam za moją głupotę. Nie zmieniłem sobie −2 na 2 w poziomej asymptocie i dziwię się, że mi nie wychodziło... Wszystko pięknie gra. Metoda wężyka i wszystko się sprawdziło przepięknie. Wielkie podziękowania dla Ciebie!