Niech X będzie dowolnym punktem leżącym wewnątrz równoległoboku ABCD.......
Magda: Niech X będzie dowolnym punktem leżącym wewnątrz równoległoboku ABCD. Udowodnij że
|AX|<|BX|+|CX|+|DX|
31 sie 16:29
b.:
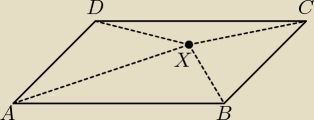
Wykorzystaj 2 razy nierówność trójkąta, np. dla trójkątów: AXD oraz BCX...
Zacznę dla trójkąta AXD:
|AX| < |DX| + |AD|
i teraz pozostaje oszacować z góry |AD|
31 sie 21:05
AS: AX + DX > AD z własności trójkąta
BX + CX > BC
Stronami odejmuję
BX + CX − AX − DX > BC − AD ale BC − AD = 0 bo BC = AD
BX + CX − AX − DX > 0
czyli
AX < BX + CX − DX
Gdy do prawej strony dodamy 2*DX to ją zwiększymy i nierówność
zostanie zachowana
AX < BX + CX + DX c.n.d.
1 wrz 09:25
b.: Stronami to lepiej ASie nierówności nie odejmuj, bo to nie działa...
przykład:
2+3 > 5
7+7 > 2
odejmujemy stronami:
2+3 − 7−7 > 5−2
−9 > 3

1 wrz 21:24
b.: oj pomyłka, zawsze zauważam takie rzeczy jak już się wysyłają

jeszcze raz przykład:
2+3 > 4 (nie od 5 !)
7+7 > 2
odejmujemy stronami:
2+3 − 7−7 > 4−2
−9 > 2

1 wrz 21:25
AS: Faktycznie!Masz rację zagalopowałem się! Brrrr!
2 wrz 09:07
AS:
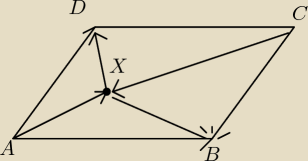
A może tak
→ → →
|AX| + |DX| > |AD| z własności trójkąta
→ → → → →
|CX| + |BX| > |CB| ale |CB| = −|AD|
→ → →
|AX| + |DX| > |AD|
→ → →
|CX| + |BX| > −|AD| stronami dodajemy
→ → → → →
|AX| + |DX| + |CX| + |BX| > 0
→ → → → → →
|BX| + |CX| + |DX| > −|AX| |−|AX|| = |AX|
stąd zależność
→ → → →
|AX| < |BX| + |CX| + |DX|
Zastępując wektory odcinkami mamy
AX < BX + CX + DX c.n.d.
2 wrz 10:52
b.: no blisko, ale są tu pewne błędy w zapisie:
→
|CB| to długość wektora, więc jest zawsze nieujemna −− równość z trzeciego wiersza jest
fałszywa
proponuję tak:
|AX| < |DX| + |AD| z nierówności dla trójkąta AXD
|AD| = |BC| < |BX| + |CX| z nierówności dla trójkąta BCX
łącząc te dwie nierówności dostajemy tezę:
|AX| < |DX| + |AD| < |DX| + ( |BX| + |CX| )
4 wrz 21:53
AS: dzięki za korektę − zauważyłem nieścisłości ale nie chciało mi się poprawiać.
5 wrz 08:44
 Wykorzystaj 2 razy nierówność trójkąta, np. dla trójkątów: AXD oraz BCX...
Zacznę dla trójkąta AXD:
|AX| < |DX| + |AD|
i teraz pozostaje oszacować z góry |AD|
Wykorzystaj 2 razy nierówność trójkąta, np. dla trójkątów: AXD oraz BCX...
Zacznę dla trójkąta AXD:
|AX| < |DX| + |AD|
i teraz pozostaje oszacować z góry |AD|

 jeszcze raz przykład:
2+3 > 4 (nie od 5 !)
7+7 > 2
odejmujemy stronami:
2+3 − 7−7 > 4−2
−9 > 2
jeszcze raz przykład:
2+3 > 4 (nie od 5 !)
7+7 > 2
odejmujemy stronami:
2+3 − 7−7 > 4−2
−9 > 2 
 A może tak
→ → →
|AX| + |DX| > |AD| z własności trójkąta
→ → → → →
|CX| + |BX| > |CB| ale |CB| = −|AD|
→ → →
|AX| + |DX| > |AD|
→ → →
|CX| + |BX| > −|AD| stronami dodajemy
→ → → → →
|AX| + |DX| + |CX| + |BX| > 0
→ → → → → →
|BX| + |CX| + |DX| > −|AX| |−|AX|| = |AX|
stąd zależność
→ → → →
|AX| < |BX| + |CX| + |DX|
Zastępując wektory odcinkami mamy
AX < BX + CX + DX c.n.d.
A może tak
→ → →
|AX| + |DX| > |AD| z własności trójkąta
→ → → → →
|CX| + |BX| > |CB| ale |CB| = −|AD|
→ → →
|AX| + |DX| > |AD|
→ → →
|CX| + |BX| > −|AD| stronami dodajemy
→ → → → →
|AX| + |DX| + |CX| + |BX| > 0
→ → → → → →
|BX| + |CX| + |DX| > −|AX| |−|AX|| = |AX|
stąd zależność
→ → → →
|AX| < |BX| + |CX| + |DX|
Zastępując wektory odcinkami mamy
AX < BX + CX + DX c.n.d.