help
k.king1969: Punkt A=(4,−3) jest wierzchołkiem kwadratu ABCD. Wiedząc że jedna z przekatnych kwadratu
zawiera się w prostej o równaniu y=1/2x wyznacz współrzędne wierzchołków tego kwadratu oraz
oblicz pole kwadratu.
18 mar 13:25
Edyta PK:
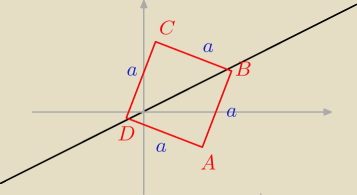
|AD|=|AB|
A=(4,−3)
B=(x
1,y
1)
D=(x
2,y
2)
√(x2−4)2+(y2+3)2=
√(x1−4)2+(y1+3)2
|DB|=a
√2
√(x2−x1)2+(y2−y1)2=
√2*
√(x2−4)2+(y2+3)2
√(x2−4)2+(12x2+3)2=
√(x1−4)2+(12x1+3)2
√(x2−x1)2+(12x2−12x1)2=
√2*
√(x2−4)2+(12x2+3)2
teraz trzeba obliczyć układ równań z dwoma niewiadomymi
podnosząc obie strony do kwadratu otrzymujemy
| | 1 | | 1 | |
(x2−4)2+( |
| x2+3)2=(x1−4)2+( |
| x1+3)2 |
| | 2 | | 2 | |
| | 1 | | 1 | | 1 | |
(x2−x1)2+( |
| x2− |
| x1)2=2*[(x2−4)2+( |
| x2+3)2] |
| | 2 | | 2 | | 2 | |
dalej spróbuj policzyć samemu
18 mar 15:37
 |AD|=|AB|
A=(4,−3)
B=(x1,y1)
D=(x2,y2)
√(x2−4)2+(y2+3)2=√(x1−4)2+(y1+3)2
|DB|=a√2
√(x2−x1)2+(y2−y1)2=√2*√(x2−4)2+(y2+3)2
|AD|=|AB|
A=(4,−3)
B=(x1,y1)
D=(x2,y2)
√(x2−4)2+(y2+3)2=√(x1−4)2+(y1+3)2
|DB|=a√2
√(x2−x1)2+(y2−y1)2=√2*√(x2−4)2+(y2+3)2