jak to obliczyc? Marcin: Wektor AB=[6, 4] jest podstawą trójkąta równoramiennego o wierzchołku C(2, 3) i wektorze wysokości CD=[−2, 3]. Znaleźć równania boków tego trójkata.

Eta: podpowiem

Eta: nie piszę strzałek nad wektorami , bo mi wygodniej( ale Ty pisz koniecznie) wektor AB = [6, 4] wektor AB=[ x_B − x_a, y_b − y_A} porównując współrzędne otrzymasz: (**) x_B − x_A = 6 ∊ y_B − y_A = 4 wektorCD = [−2, 3] podobnie ; otrzymasz współrzedne punktu D ( −4, 6) teraz wiemy ,że D jest środkiem odcinka AB ( bo trójkąt jest równoramienny. korzystajac ze wzoru na współrzędne środka otrzymasz następne równania:

xA + xB		yA +yB
	= −4 ∊		= 6
2		2

to(***) x_A +x_B = − 8 i y_A + y_B = 12 rozwiąż układy równań (**) i (***) otrzymasz współrzędne punktów A i B równania prostych , w których zawierają sie boki trójkąta już potrafisz z pewnością wyznaczyć

Eta: Poprawiam, D( 0, 6) .....

Eta: poprawne współrzedne wierzchołków trójkąta: A( − 3, 4) B( 3, 8) C( 2, 3) i środek boku AB : D( 0,6) popraw , bo w tym co podałam wyżej pomyliłam współrzedne punktu D PS: przepraszam ,ale to już zmęczenie daje znać ,że pora spać

Eta: równania prostych: pr. AB : y = ²₃ x +6 pr. AC: y= −¹₅x +¹⁷₅ pr. BC: y= 5x +7 można więc stwierdzić ,że trójkąt jest równoramienny i prostokątny kąt C = 90^o bo proste AC i BC są prostopadłe bo współczynniki kierunkowe: a₁ = −¹₅ i a₂ = 5 to: a₁ *a₂ = −1 Dobranoc, miłych snów

Marcin: dzieki wielkie sam to bym sobie z tym nei poradzil

Marcin: tylko jeszcze prosta BC ma zle rownanie bo powinno byc y= −x + 5

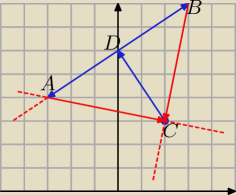
Bogdan: Można również tak (także nie zaznaczam strzałek nad wektorami): Zaznaczamy punkt C = (2, 3). Z tego punktu prowadzimy wektor CD = [−2, 3] (2 w lewo, 3 do góry). Mamy punkt D = (X_D, y_D). [x_D − 2, y_D − 3] = [−2, 3] ⇒ x_D = 0, y_D = 6, D = (0, 6).

	1
Z punktu D prowadzimy wektor		AB = [3, 2]. mamy punkt B = (xB,yB).
	2

[x_B − 0, y_B − 6] = [3, 2] ⇒ x_B = 3, y_B = 8, B = (3, 8).

	1
Z punktu D prowadzimy wektor −		AB = [−3, −2]. mamy punkt A = (xA,yA).
	2

[x_A − 0, y_A − 6] = [−3, −2] ⇒ x_A = −3, y_B = 4, A = (−3, 4).