ktos pomoze z takim zadaniem? Marcin: Na paraboli y²=24x dany jest punkt odległy od ogniska o 14. Znaleźć odległość d tego punktu od wierzchołka paraboli.

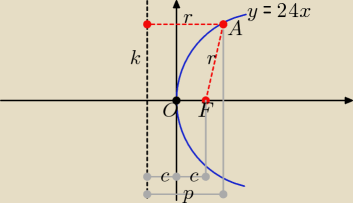
Bogdan: Ten rysunek powinien pomóc. y² = 2px k − kierownica F = (c, 0) − ognisko O = (0, 0)

	p
c =
	2

r = IAF| = 14 Oblicz współrzędne punktu A(x_A,y_A) i następnie d = |AO| = √x_A² + y_A²

Bogdan: Na rysunku źle wpisałem wzór paraboli, poprawiam: y² = 24x

Marcin: a na wikipedi rownanie na Parabola z poziomą osią symetrii wyglada tak: (y−h)² = 4p(x−h) h=0 to dlaczego napisales : y² = 2px pomylka?

Bogdan: Jeśli są różne zapisy dotyczące jakiegoś pojęcia, to wcale nie znaczy, że jeden z tych zapisów jest błędny. W informacji, którą podałem, nie ma pomyłki, a Ty skorzystaj z tego lub nie. Radzę uzupełnić podstawowe wiadomości z geometrii analitycznej. http://www.wsipnet.pl/oip/msl/cz2/u/wgks.html

Bogdan: http://oen.dydaktyka.agh.edu.pl/dydaktyka/matematyka/a_matem_1_rok/geometria/repetyt/node37.html

Marcin: no dobrze tylko tak mowie wiec na wikipedi jest blad co czesto tam sie zdaza

Bogdan: Jeszcze raz podkreślam: jeśli są różne zapisy dotyczące jakiegoś pojęcia, to wcale nie znaczy, że jeden z tych zapisów jest błędny. Żeby wyrokować o błędzie, trzeba go najpierw wskazać i uzasadnić. Nie wyprowadzaj wniosku o błędzie, jeśli przedtem nie uzasadnisz tego wniosku. Jeśli stwierdzasz błąd na Wikipedii, to wykaż, że tak jest. Jeśli jednak tego nie potrafisz, to nie mów o błędzie.

Eta: Zlituję się

	p
2p = 24 =>		= 6 to F( 6,0)
	2

	p
r= x +		( uzasadnij tę zalezność )
	2

to x +6 = 14 => x = 8 zatem: y² = 24 *8 => y= 8√3 lub y = −8√3 A₁( 8, 8√3) , A₂( 8, −8√3) −−− są dwa takie punkty symetryczne względem osi OX IA₁OI²= IA₂OI² = 8² + (8√3)² = 64 + 3*64 = 4*64 to; IA₁OI = IA₂OI = 16

Eta: Dobry wieczór Bogdanie Uśmiechnij się , szkoda zdrowia !

Basia: Witajcie! Równanie podane w Wikipedii, które nawiasem mówiąc ma postać (y−h)² = 4p(x−k) dotyczy paraboli, której wierzchołek znajduje się w punkcie P(k,h) i dla której osią symetrii jest prosta y=h, a odległość ogniska od kierownicy jest równa 2p. W tej (bardzo rzadko) używanej postaci ognisko = F(k+p,h) kierownica x=k−p Gdybyś poczytał dokładnie dowiedziałbyś się, że jest ono równoważne z równaniem (y−h)²=2d(x−k) gdzie d oznacza odległość ogniska i kierownicy. Wtedy ognisko = F(k+^d₂,h) kierownica x=k−^d₂ Bogdan użył najpowszechniej stosowanego dla paraboli o wierzchołku w punkcie O(0,0) i osi symetrii pokrywającej się z osią OX równania postaci y²=2px gdzie p oznacza odległość ogniska od kierownicy, i słusznie, bo w tym zadaniu najwygodniej z niego skorzystać. Pozdrawiam

Bogdan: Dobry wieczór Eto . No właśnie uśmiechnąłem się czytając słowa Marcina. Są one potwierdzeniem diagnozy stanu wiedzy i umiejętności polskich uczniów, jaka została wczoraj opublikowana po podsumowaniu tegorocznych egzaminów w szkołach podstawowych, gimnazjach i szkołach ponadgimnazjalnych. Można w tej sprawie znaleźć artykuły i komentarze w wczorajszym wydaniu "Dziennika", zacytuję tylko jedno zdanie z opinii MEN: nasi uczniowie są niesamodzielni, nie kojarzą faktów, nie wyciągają wniosków. Zanosi się na kolejne reformy oświaty.

Basia: I po kolejnych reformach będzie jeszcze gorzej !

Eta:

Bogdan: Witaj Basiu, uprzedziłaś mnie wyjaśniając zapis w Wikipedii. Dodam dla Marcina informację, że zapisy (x − p), (y − q) oznaczają przesunięcie figury o wektor [p, q].

Bogdan: http://www.dziennik.pl/wydarzenia/spoleczenstwo/article437755/Kolejna_wielka_reforma_oswiaty.html

Basia: Przeczytałam te artykuły. To już naprawdę nie mieści się w głowie. Możliwe, że uczniowie nie popisali się ani wiedzą, ani umiejętnością logicznego myślenia (wymaganie od nich, przy obecnych programach myślenia abstrakcyjnego jest abstrakcją do n−tej potęgi i kompletną utopią), ale czym popisali się egzaminatorzy, którzy nie są w stanie zauważyć, że zaprzysiężenie i odebranie przysięgi to pojęcia równoznaczne ? Czym popisała się OKE, która reklamacji nie uwzględniła tłumacząc się, że odpowiedź musi być zgodna z kluczem czyli z dokładnością do kropki i przecinka wykuta na pamięć z podręcznika ? Czym popisała się CKE, która również reklamacji nie uwzględniła tłumacząc się z kolei tym, że...... musiałaby zalecić ponowne sprawdzanie arkuszy w całym kraju ? I czym w końcu popisała się pani minister Hall, która udaje, że nie widzi w tym żadnego problemu, nie reaguje i nie zajmuje żadnego stanowiska ? To nie jest matura. To są kpiny. Myślałam, że ostatni przypadek nie uznania odpowiedzi, że żołnierz ma prawo użyć broni w obronie własnej, bo w regulaminie napisano w obronie własnego życia miał miejsce w carskiej Rosji i dotknął niejakiego Melchiora Wańkowicza. Okazuje się, że system oświatowy III RP "przebił" nie tylko PRL. Carską Rosję również, bo tam odpowiedzi nie uznał jakiś "didka" (stopnia nie pomnę, ale jakiś bardzo niski), natomiast kapitan reklamację rekruta Wańkowicza jednak uwzględnił.

Bogdan: Zgadzam się z poglądem mówiącym o obniżeniu się poziomu szkolnictwa wraz z jego umasowieniem. Dobranoc.