narysuj wykres funkcji, omów jego własności.
wajdzik: Narysuj wykres funkcji i na jej podstawie omów własności tej funkcji:
D=R\{−2}
| 3(x+2)−7 | | 3(x+2) | | 7 | | −7 | |
| = |
| − |
| = |
| +3 |
| x+2 | | x+2 | | x+2 | | x+2 | |
W: [−2,3]
Mógłby ktoś narysować ostatnie odbicie na wykresie? Ja SPRÓBUJĘ narysować bo na tej stronie
jeszcze nie nauczyłem się rysować.
A co do własności:
D=R\{−2}
Z
w=R\{3}
Funkcja różnowartościowa
Funkcja nie jest okresowa
Zgadza się?
Ktoś by tutaj coś jeszcze dołożył?

Z góry dziękuję za pomoc.
17 mar 13:01
Eta:
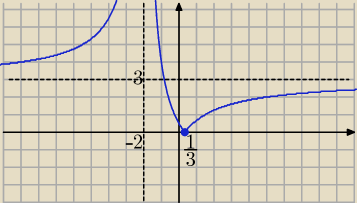
17 mar 13:06
wajdzik:
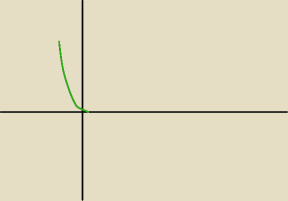
jest ok ?
17 mar 13:06
wajdzik: Dzięki Eta, widzę, że nawet mi to wyszło. A co do własności? jest git?

17 mar 13:07
wajdzik: 
17 mar 13:09
wajdzik: 
17 mar 13:12
wajdzik: 
17 mar 13:15
Cusack: asymptoty i monotoniczność jeszcze dopisz.
17 mar 13:17
Cusack: patrząc na wykres Ety, to funkcja nie jest różnowartościowa.
Zbiór wartości też do poprawy.
17 mar 13:20
wajdzik: Cusack, nie rozumiem czemu ona nie jest różnowartościowa oraz czemu zbiór wartości jest do
poprawy. Mógłbyś mi to jakoś pokazać?
Asymptota pionowa y=−2
Asymptota pozioma y=3
f.rosnąca x∊(−∞,−2), x∊(−2,+∞)
17 mar 13:35
wajdzik: 
17 mar 13:41
krystek: A pomyśl , gdzie się podnosisz w górę , a gdzie spadasz w dół?
17 mar 13:43
wajdzik: Rozumiem już co zrobiłem źle jeśli chodzi o różnowartościowość. A zbiór wartości... może coś
takiego:
| | 1 | |
y∊R\{−U{1}{2, |
| . (stwierdzam, patrząc na wykres). |
| | 2 | |
17 mar 13:48
krystek:
f↗⇔x∊
f↘⇔x∊
a zb wartości to y∊<0,∞) do wykresu Ety
17 mar 13:52
asdf: Wajdzik, oblicz asymptoty i ekstrema. Zaznacz kiedy funkcja maleje, a kiedy rośnie. Znajdz
miejsca zerowe. Dla wartości < 0 odbij to wzgledem OX (w tym przypadku od miejsca zerowego w
prawo odbijasz)
17 mar 13:54
krystek: @asdf to poziom LO
17 mar 13:56
asdf: i tak dla przypomnienia: miejsce zerowe liczysz z licznika, a asymptote sprawdzasz na krancach
dziedziny (tutaj wazny jest mianownik) )
17 mar 13:56
asdf: ...wlasnie dlatego nie lubialem matematyki w LO, wszystko na okolo.
17 mar 13:56
wajdzik:
f↗⇔x∊(−
∞,3) U (3,+
∞)

17 mar 13:56
krystek: Xle podnosisz sie w górę gdy x∊(−∞,−2) oraz dla x∊< dokończ
spadaszw dół dla x∊(−2,?>
17 mar 13:59
wajdzik: JA POWIEM, że nienawidzę systemu szkolnego, nie powinno być "GIMBAZY" bo to tylko
opóźnia rozwój dziecka. 7 klas podstawówki i do liceum(gdzie nie powinno byc 16 przedmiotów)
ja mając 5 matematyk w tygodniu jestem całkowicie w tyłku. Na lekcji NIC nie robimy a sam muszę
robić DOSŁOWNIE WSZYSTKIE zadania w domu. Wkurza mnie to, że naród chce mieć tępy naród.
17 mar 13:59
wajdzik: | | 1 | |
dla x∊(−2,+∞) ? a spadam w dół dla x∊(−2, |
| )? |
| | 3 | |
17 mar 14:01
17 mar 14:02
wajdzik: ASDF, dzięki. Wszystko co mi napisałeś rozumiem i tak się kieruję nie licząc ekstrema. Tego wgl
JESZCZE nie brałem.
17 mar 14:02
krystek: | | 1 | |
f↗ jeszcze dla x∊< |
| ,∞) |
| | 3 | |
17 mar 14:03
wajdzik: Dopóki walczę, jestem zwycięzcą. Najgorsze jest to, że nie jestem w stanie się tak wyrobić żeby
dotknąć zbioru zadań. Nie wiem kiedy ja to zrobię. Pewnie w wakacje będę się musiał złapać za
jaja i to wszystko nadrabiać.
17 mar 14:04
wajdzik: | | 1 | |
Krystek, ale czemu od < |
| ? Brałeś to z wykresu Ety, ale Ona nie przerysowała tego co jest |
| | 3 | |
pod osią OX, i dlatego myślałem, że od (2,+
∞). Czemu nie rysujemy tego co ma być pod osią OX?
17 mar 14:06
krystek: y=I....I więc wszystko nad osia OX
17 mar 14:07
wajdzik: Ok, wszystko rozumiem. Dzięki, zabieram się za kolejne przykłady.
17 mar 14:10
17 mar 14:16
asdf: @Wajdzik
Ja w technikum miałem po 2 godziny w tygodniu matematyke, a na studiach z powodzeniem zdalem
sesje z matmy. Jak będziesz pracowac i nawet robic niektore rzeczy ponad program to zobaczysz,
ze Ci się to przyda − im więcej widzsz rozwiązan jednego zadania tym lepiej

17 mar 15:00
 Z góry dziękuję za pomoc.
Z góry dziękuję za pomoc.

 jest ok ?
jest ok ?












