znak funkcji Klaudia: jak zbadać znak funkcji: y=^x2−2x+25_(x−1)²

krystek: licznik zawsze dodatni a mianownik (x−1)² jaki ?

Klaudia: no tu wychodzi ze D = R/{1} czyli ta funkcji jest dodatnia w calej swojej ddziedzinie?

Klaudia: no tu wychodzi ze D = R/{1} czyli ta funkcji jest dodatnia w calej swojej ddziedzinie?

krystek: Tak

Klaudia: a jak to zapisać tak żeby tak formalnie było ?

krystek: tak jak podałyśmy Licznik + dla każdego x ( ponieważ Δ<0 i a>0) mianownik + w całej dziedzinie Iloraz dwóch wyrażeń dodatnich jest dodatni.

Klaudia: okej dzieki za pomoc

Klaudia: a jak policzyć pochodną tej funkcji? mi wyszlo: y=^−40x+48_{((x−1)²)²} ale nie wiem czy dobrze

krystek: Zapisz ja nie liczę Pochodna ilorazu

Klaudia: f'(x)=^{(x2−2x+25)'(x−1)2−[(x2−2x+25)((x−1)2)']}_{((x−1)²)²} = ^{(2x−2)(x2−2x+1)−(x2−2x+25)(2x−2)}_{((x−1)²)²}=i po przemnozeniu tego wychodzi taki wynik jak mi ale nie wiem czy tj dobrze

Klaudia: f'(x)=^{(x2−2x+25)'(x−1)2−[(x2−2x+25)((x−1)2)']}_{((x−1)²)²} = ^{(2x−2)(x2−2x+1)−(x2−2x+25)(2x−2)}_{((x−1)²)²}=i po przemnozeniu tego wychodzi taki wynik jak mi ale nie wiem czy tj dobrze

krystek: Pisz przy ułamku duże U

krystek: Liczysz poprawnie

Klaudia:

	(x2−2x+25)'(x−1)2−[(x2−2x+25)((x−1)2)']
f'(x)=		=
	((x−1)2)2

	(2x−2)(x2−2x+1)−(x2−2x+25)(2x−2)
		=
	((x−1)2)2

	2x3−4x2+2x−2x2+4x−2−(2x3−2x2−4x2−4x+50x−50)
	((x−1)2)2

krystek: w drugim nawiasie +4x winno być

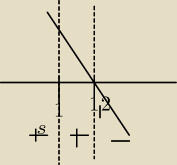
Klaudia: i żeby policzyc ekstermum funkcji to f'(x) przyrównuje do zera

−40x+48
	= 0
((x−1)2)2

−40x+48=0

	1
x=1		orki za ten nieudolny wykres ale chcialam jeszcze zapytac czy dobrze wyznaczylam to
	5

max?

krystek: Tak

Klaudia: ale gdzie to +4x?

Klaudia: ale gdzie to +4x?

Klaudia: ale gdzie to +4x?

krystek: −2x*(−2) gdy wymnażałaś

Klaudia:

	−48x−48
ahaa rzeczywiscie to teraz jest takie równanie pochodnej :
	((x−1)2)2

czyli x= 1 i max tej funkcji bedzie w pkt 1?

Klaudia: +48*

Klaudia: bo ta 1 jest tez wyrzucona z dziedziny i nie wiem czy to tak moze byc ?

krystek: 1 nie należy do D_f' Zbadaj granice x→1₊ i x→1₋ w otoczeniu będzie malała i rosła

Klaudia: to dla 1+ podstawiamy liczbe troche wieksza od 1 i bedziemy miec granice +∞ i dla 1− wychodzi mi taka sama ta granica wiec chyba zle

krystek: Ok dobrze .

Klaudia: ahaa ale dalej nie wiem co zrobić z tym max ?

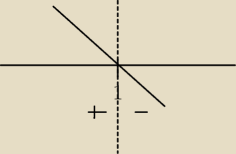
Klaudia: taki bedzie ten wykres ?

krystek: Funkcja nie posiada max ponieważ f' nie jest =0 dla żadnego x. obliczyć możesz tylko jej monotonicznośc.

krystek: Poprawnie OKREŚLIĆ MOŻESZ JEJ MONOTONICZNOŚĆ>

Klaudia: ahaa czyli ona nie ma ani max ani min? jest rosnąca (−nies,1) i malejąca od (1, + nies) ?

krystek: A le Ty dałaś wykres funkcji liniowej y=ax gdy a<0

Klaudia: noobo ja juz nie wiem jak to zrobić wyszlo mi 1 które jest wyrzucone z dziedziny a wykres zaczełam rysować od dołu bo przy x jest −

krystek: f↗⇔f'>0⇔.....⇔−48x−48>0⇔−48x>48⇔x<−1 f↘⇔f'<0⇔.... x>−1 z wyłączeniem 1

krystek: A wyjściowe pytanie masz żle postawione . "zbadać znak funkcji ?"

Klaudia: ogólnie to mam zbadac przebieg zmiennosci tej funkcji i w 2 podpunkcie mialam zbadac znak funkcji a teraz utknełam na tej pochodnej bo wyszla ta 1

krystek: Nie badasz znaku funkcji tylko znak pochodnej. Ponieważ gdzie pochodna dodatnia tam funkcja rośnie . zapisałam Tobie symbolicznie o 15:21

krystek: W LO miałaś m zerowe f wymiernej

W(x)
	=0 ⇔W(x)=0 i p{x)≠0
p(x)

Klaudia: a moglabys mi napisac odpowiedzi do monotonicznosci tej funkcji ?

krystek: 15:21 zapisałam