prawdopodobienstwo Alois~: 1)Wykaż że jesli A⊂Ω i A' jest zdarzeniem przeciwnym do zdarzenia A , to P(A')=1−P(A) nie wiem czy to jest dobrze bo ja nie ogarniam tego ale próbowałam więc: P(Ω)=1 P(Ω)−P(A)=P(A') 1−P(A)=P(A') 2)Wykaż że jeśli A,B ⊂Ω i A⊂B, to P(A)≤P(B) a tu już gorzej 3)Wykaz ze jesli A, B ⊂Ω to P(AUB)=P(A)+ P(B)−P(A∩B)

PW: 3 warunki, jakie z definicji musi spełniać funkcja P, żeby można ją nazwać prawdopodobieństwem: 1° P(A)≥0 dla wszystkich A⊂Ω 2° P(Ω)=1 3° dla dowolnych A, B⊂Ω PA∩B=∅ ⇒P(AUB)=P(A)+P(B). Dowód 1) Wiadomo, że z definicji AUA'=Ω oraz A∩A'=∅. Zastosowanie warunku 3° definicji prawdopodobieństwa daje (a) P(AUA')=P(A)+P(A'), a warunku 2° (b) P(AUA')=P(Ω)=1. Porównanie prawych stron (a) i (b) pozwala stwierdzić, że P(A)+P(A')=1, co kończy dowód.

Alois~: czyli to co ja rozpisałam w 1 by nie uznali jako dowod ? i jest źle ?

PW: Nie, bo w gruncie rzeczy korzystasz z tezy. Wzór ten jest tak silnie "przyswojony" przez większość ludzi, że uważają go za coś oczywistego − tak jakby część definicji prawdopodobieństwa, nieraz dziwią się − jak to, to wymaga dowodu? Wyjaśnienie może być tylko takie: warunki 1°, 2°, 3° to definicja, reszta wymaga dowodu. Dowód wymaga więc zastosowania definicji, co zrobiliśmy. Ty nie powoływałaś się na definicję, zatem − niezależnie od tego jak myślałaś − dowód nie byłby uznany. Zauważ, że tak zwana klasyczna definicja prawdopodobieństwa to też nie jest żadna definicja, lecz proste twierdzenie, którego dowód wynika właśnie z zastosowania definicji prawdopodobieństwa 1°, 2°, 3°. Nazwa "klasyczna definicja prawdopodobieństwa" ciągnie się − w sposób mylący − ze względów historycznych.

Alois~: a jak pozostałe sensownie udowodnić? ( zaraz spr tez sama to 2 i 3 moze cokolwiek w miare wyjdzie )

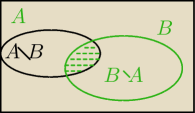
Mila: 3)Wykaz ze jesli A, B ⊂Ω to P(AUB)=P(A)+ P(B)−P(A∩B) a) A i B zbiory rozlączne, A∩B=Φ P(A∩B)=0 P(AUB)=P(A)+P(B)−P(A∩B) b) A∩B≠Φ Szkic P(AUB)=P(A\B)+P(A∩B)+P(B\A) =suma zbiorów rozłącznych =P(A)−P(A∩B)+P(A∩B)+P(B)−P(A∩B)= =P(A)+P(B)−P(A∩B)

Alois~: dzięki Mila

Mila: Myślałam, że niepotrzebnie to pisałam, bo nie dałaś znaku, że to czytasz.