. asdf: Wskaż punkty, w których funkcja moze miec ekstremum y = 3 − ³√x, D: x ∊ (−∞;∞)

	1
y' = −		, D: x ∊ (−∞;0)(0;∞)
	33√x2

przyrównuję do zera:

	1
−		= 0
	33√x2

odp: moze miec w punkcie x = 0?

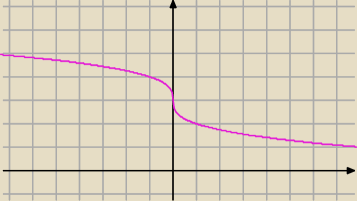
Aga1.: Jaki jest warunek konieczny istnienia ekstremum?

asdf: f'(x₀) = 0 funkcja ma ekstremum lokalne w x₀ (a tego nie wiem czy ma czy nie ma)

asdf: Nie zrozumiały dla mnie przykład dziedzina pochodnej to x != 0, Uwaga 3. Funkcja ma ekstremum lokalne tylko w punktach, w których pochodna jest równa zeru albo w punktach, w ktorych pochodna nie istnieje. czyli w punkcie x₀ "moze istniec" ekstremum?

asdf: jeszcze probuje tak to zrozumieć:

	1
−		> 0
	33√x2

1
	< 0
33√x2

3³√x² > 0 x^2/3 > 0 ale nie wiem co to mi dalo

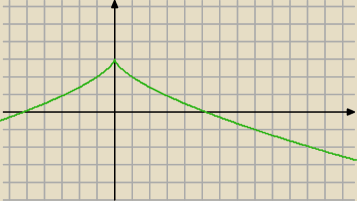
asdf: a tu widać, ze ma ekstremum

PW: Policzenie pochodnej nie daje odpowiedzi dla x₀=0, bo w tym punkcie nie ma pochodnej. Sytuacja jest analogiczna jak dla funkcji g(x)=|x|, która akurat w zerze ma minimum. W tym sensie asdf masz rację − badana funkcja może mieć ekstremum w zerze (ale nie musi). Twierdzenie o warunku koniecznym istnienia ekstremum tego przypadku nie rozstrzyga − nie ma tutaj zastosowania, bo nie są spełnione jego założenia. Rozstrzygnięcie dla x₀=0 musi nastąpić z zastosowaniem innych metod. W tym szczególnym wypadku łatwo jest elementarnym sposobem pokazać, że f jest malejąca na całym zbiorze liczb rzeczywistych.

asdf: Ok, ale nie zgodze się z tym, że f jest malejąca na całym zbiorze liczb rzeczywistych

Mila: Pochodna jest ujemna. Funkcja malejąca . Na rysunku z 22:39 pochodna zmienia znak, po przejściu przez x=0, w którym nie istnieje.

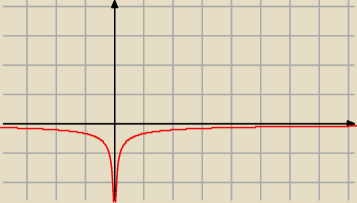
asdf: Pochodna jest ujemna w cały zbiorze, ale zmienia monotoniczność w zerze, jak to udowodnić?

PW: f(x)=3−³√x jest malejąca. ³√x jest odwrotna do rosnącej x³ (powszechnie znane), a więc jest rosnąca, wobec tego −³√x jest malejąca (po dodaniu 3 też).

Mila: Napisz wzór funkcji z 22:52,

asdf: wzór funkcji z 22:52 to pochodna funkcji:

	1
y = −		i, że jest ona ujemna w całym zbiorze to wiadomo − w mianowniku x2 nie
	33√x2

zmienia znaku na ujemny, a całość jest ujemna − więc funkcja jest < 0 @PW Jest malejąca, ale w takim razie skąd się tam wziely 2 miejsca zerowe, funcja rosna do 0, malejąca od 0 itd..

PW: Ten zielony wykres jest zły (pierwiastek trzeciego stopnia z liczby ujemnej jest ujemny, po lewej stronie zera wartości funkcji są większe od 3). A zrób tak "po szkolnemu" x³, odwrotna do niej (symetria wzgl. osi y=x) i przesunąć w górę 0 3 − Aga dała dobry wykres, który wprawdzie się nie przecina z osią OX, ale to dlatego, że nie starczyło miejsca na rysunku.

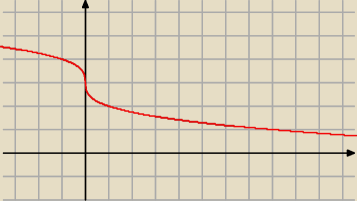
asdf: Już wiem, czemu tak błądziłem, napisałem: y = 3 − ³√x² .. i teraz widać, że mogę wziąć ten punkt x₀ pod uwagę (poniewaz wykracza poza dziedzine pochodnej), ale patrząc na wykres w tym punkcie nie ma ekstremum tak?

PW: Poprawka: x³ → odwrotna do niej → przeciwna (minus) → dodać trzy

PW: Oczywiście, że nie ma. Funkcja jest malejąca, nie ma ekstremów.

asdf: Przez własną głupote sie chyba najwiecej naucze. Dzieki, a teraz mam taki przykład: y = ³√x²*e^−x D to R

	2		2
y' =		*e−x − e−x*3√x2 = e−x(		−3√x2)
	33√x		3√x

D: x > 0

	2
e−x(		−3√x2) = 0 // e−x (f. wykł jest > 0)
	3√x

z U{2}{3√x − ³√x² = 0

2 − 3√x2*3√x
	= 0
33√x

2−3x
	= 0
33√x

3³√x(2−3x) = 0 x = 0

	2
x =
	3

D: x > 0

	2
czyli funkcja ma ekstremum w		, czy w x = 0 tez?
	3

asdf: z lematu monotonicznosci, musi zachodzić: sgn [ lim_x−>x0⁺ f(x) ] ≠ sgn [lim_x−>x0⁻ f(x) ] P.S moze zapis nie dokladny, ale chyba wiadomo o co chodzi