POMOCY! henio: W trapezie równoramiennym ABCD podstawa CD ma długość 1, kąt ABC ma miarę 60, a przekątna AC jest prostopadła do boku BC. Oblicz objętość bryły powstałej z obrotu trapezu wokół boku BC.

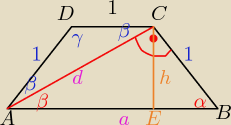
Edyta PK: po obrocie otrzymamy "ścięty" stożek o promieniu podstawy równym r=a objętość obliczymy jako różnicę objętości całego stożka i górnej części stożka (rysunek za chwilę) α=60^o β=30^o ponieważ kąty przy tym samym ramieniu mają w sumie 180^o, więc kąt ACD równa się β=30^o ponieważ kąty przy podstawie są równe, więc kąt DAC też równa się β=30^o, stąd γ=120^o i trójkąt ACD jest równoramienny przekątną trapezu policzymy z twierdzenia sinusów

d		1
	=
sinγ		sinβ

d		1
	=
sin120o		sin60o

d=√3 a²=(√3)²+1² a=2

	1
|EB|=
	2

	1
h2+(		)2=12
	2

	√3
h=
	2

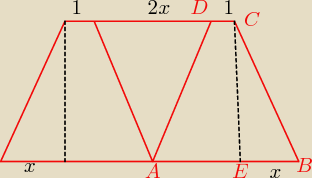Edyta PK: mam nadzieję, że dobrze wyobrażam sobie tę bryłę, która powstanie cięty stożek z dziurą w środku objętość obliczę jednak z walca nie ze stożka, będzie prościej V=πr²*h

	1
x=|ED|=
	2

	1+2x+1
r=
	2

	3
r=
	2

	3		√3
V=π* (		)2*
	2		2

	9
V=		√3π [j3]
	8

Mila: Henio, masz odpowiedź? Edytko, trochę inaczej sobie wyobrażam tę bryłę. Nie wiem, czy zdołam narysować, bo UPC ciągle mi wysiada. To zrobię jutro, bo już nie mam cierpliwości do dzisiejszego internetu. Pozdrawiam.

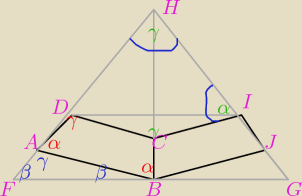Edyta PK: racja Mila, to będzie wyglądało raczej tak (ta czarna część) przekrój przez środek stożka sory za jakość rysunku nie mam wprawy Trójkąt FBA jest równoramienny |AF|=|AB|, podobnie trójkąty DCI i DIH α=60^o γ=120^o β=30^o kąty ustaliłam z kątów przyległych Objętość figury otrzymanej z obrotu równoległoboku to różnica objętości stożka o przekroju FGH i sumy objętości stożków o przekroju DCI, DIH, FBA i BGJ, przy czym FBA i BGJ są takie same za chwilę reszta, muszę zrobić dodatkowy rysunek

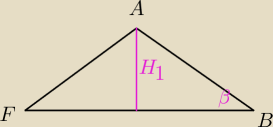Edyta PK: |AB|=a=2 (obliczone wyżej)

H1
	=sin30o
2

H₁=1

1
	|FB|=r1
2

r1
	=cos30o
2

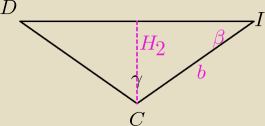
r₁=√3 V₁= πr₁H₁ V₁=3π będą dwa stożki o tej objętości

Edyta PK:

	1
r2=		|DI|
	2

b=1

H2
	=sin30o
b

	1
H2=
	2

r2
	=cos30o
b

	√3
r2=
	2

	1
V2=		πr22H2
	3

	1
V2=		π
	8

poprzednio we wzorze zgubiłam kwadrat i jedną trzecią V₁=π

Edyta PK:

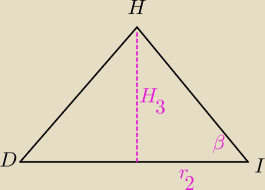
H3
	=tgβ
r2

	3
H3=
	2

	1
V3=		πr22H3
	3

	3
V3=		π
	8

dla stożka o przekroju FGH r=|FB| (rysunek z godz.7.35) r=|FB|=2r₁=2√3 (rysunek z godz.7.45) H=|CB|+H₂+H₃ H=3

	1
V=		πr2H
	3

V=12π

	1
objętość szukanej figury wynosi V−(V1*2+V2+V3)= 9		π [j3]
	2