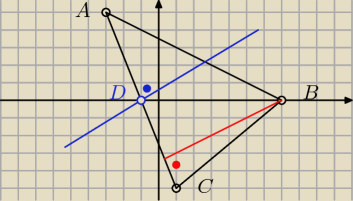
Analityczna Tereska655: Napisz równanie prostej, w której zawiera się wysokość trójkąta ABC poprowadzona z wierzchołka B oraz równanie symetralnej boku AC, jeśli A=(−3,5) B=(7,0) C=(1,−5).

dero2005: liczę współczynnik a prostej AC

	yA−yC		5+5		10		10
aAC =		=		=		= −
	xA−xC		−3−1		−4		4

licze prostą przchodzącą przez punkt B i prostopadłą do prostej AC − liczę współczynnik kierunkowy a₁*a = −1

	−1		4
a1 =		=
	10   −   4		10

− licze prostą

	4		28
y = a1(x − xB) + yB = 410(x − 7) + 0 =		x −
	10		10

dero2005: liczę punkt D

	xA+xC		yA+yC
S = (		) , (		)
	2		2

S = (⁻³⁺¹₂) , (⁵⁻⁵₂) S= (−1 , 0) − liczę współczynnik kierunkowy(warunek prostopadlości do prostej AC) a₂*a = −1

	−1		−1		4
a2 =		=		=
	a		−10   4		10

licze prosta symetralną (przechodzącą przez punkt D i prostopadły do AC)

	4		4		4
y2 = a2(x − xD) + yD =		(x +1) +0 =		x +
	10		10		10

	4		4
y =		x +
	10		10