prawdopodobienstwo matura 2012 maj rozszerzenie Alois~: Zdarzenia losowe A,B są zawarte w Ω oraz P(A∩B')=0,7. Wykaż że P(A'∩B)≤0,3 tutaj rozwiązanie już jest, bo to z majowej matury 2012 ale ja kompletnie tego prawdopodobienstwa nie łapie ! dopoki opiera sie na podstawowych wzorach z tablic to tak, a potem już niestety nie i nie wiem z czego jak mam korzystać. ( http://fakty.interia.pl/raport-matura-2012/news-matura-2012-arkusze-i-rozwiazania-zadan-z-matematyki-poziom-,nId,916157 )

Dominik: https://matematykaszkolna.pl/strona/1060.html prawo de morgana P((A∩B')') = P(A'∪B) = 0,3 wiemy, ze (A'∩B)⊂(A'∪B) c.n.w.

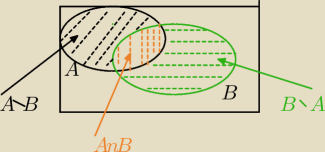
Mila: Wyjaśniam dowód z linka. Powtórz działania na zbiorach. A∩B część wspólna (iloczyn zbiorów) A\B − różnica zbioru A i B B\A −różnica zbioru B i A Te trzy zbiory są rozłączne, zatem (1) P(AUB)=P(A\B)+P(A∩B)+P(B\A) W zadaniu masz dane P(A∩B')=0,7 ale A∩B'=A\B patrz na ilustrację,(część wspólna zbioru A i dopełnienia zbioru B) Szukasz: P(A'∩B) A'∩B=B\A (część wspólna zbioru B i dopełnienia zbioru ) Korzystamy z (1) i własności, że P(AUB)≤1 P(A\B)+P(A∩B)+P(B\A)=0,7+P(A∩B)+x⇔ 0,7+P(A∩B)+x≤1 x+P(A∩B)≤1−0,7 x+P(A∩B)≤0,3 a ponieważ P(A∩B)≥0 to x≤0,3. cnw