(-3x-1)^2 czupakadabra : (−3x−1)² : witam chciałbym się upewnić czy tutaj stosuję wzór (a−b)² ? wyszło mi 9x² − 6x +1

zerohunter: No to teraz chyba delta co nie?

czupakadabra : tak tak tylko chodzi mi czy dobrze to rozwiązałem czy ten − przed 3 coś mi zmienia

Artur_z_miasta_Neptuna: ale po co delta źle ... + 6x winno być

akante: −3x to a a b to 1

Artur_z_miasta_Neptuna: zmienia ... (−3−x)² = (−(3+x))² = (−1)²*(3+x)² = 1*(3+x)² = (3+x)²

czupakadabra : Dzięki Artur

akante: chcialbym tak wszytko widziec matematycznie jak artur

czupakadabra : Ciekawe czy to dar od boga czy efekt ćwiczeń

Artur_z_miasta_Neptuna: i jedno i drugie ale przede wszystkim −−− efekt ćwiczeń

czupakadabra : ja teraz siedzę nad analityczną ... i no szlag mnie trafia bo bardzo chcę .. mogę siedzieć przed matmą długo ale nie mam pomysłu czasami .... żadnego

Artur_z_miasta_Neptuna: czasami wystarczy świeże spojrzenie na zadanie −− przejdź się z psem na spacer ... zapalić papieroska ... napić się coli i wróć a jeżeli nie ... to niestety pozostaje tylko ćwiczyć, ćwiczyć i jeszcze raz ćwiczyć

czupakadabra : Chyba zacznę palić

czupakadabra : Ej napisałbym Ci jedno zadanie z analitycznej i pokazał jak robię sprawdziłbyś czy chociaż idę dobrym tokiem ?

Fixed: Podawaj to zobaczymy

Artur_z_miasta_Neptuna: to dawaj

akante: logiczne myślenie w dzisiejszych czasach to czasami dar a czasami przekleństwo

Artur_z_miasta_Neptuna: dar −−− jesli chodzi o pracę przekleństwo −−− jeżeli chodzi o relacje damsko−męskie

czupakadabra : Punkty A( 1, √3) , B= (5, 5{3}) sąwierzchołkami trójkąta równobocznego. Wyznacz współrzędne wierzchołka C. Więc tak obliczyłem odległość AB wynosi 8. Skoro jest to trójkąt równoboczny więc odległość CB i AC też muszą być równe 8. W odległości między AC zacząłem liczyć podstawiając √(x−1)²+(y−√3)²=8 to wyszło mi ( podniosłem wszystko do kwadratu by pozbyć się piewiastka ) x²−2x+y²−2√3y=60 a w odległości między BC √x−5)²+(y−5√3)²= 8 −−−> x²−10x+y²−10√3y=−36 Jest jakiś sens ?

Artur_z_miasta_Neptuna: zrobiłbym to inaczej (prościej ... tak mi się wydaje) nie ma co sie bawić w pierwiastki z sumy kwadratów w trójkącie równobocznym ... wysokość spada na podstawę gdzie oczywiście wysokośc jest prostopadła do podstawy ile wynosi wysokośc w trójkącie równobocznym

Artur_z_miasta_Neptuna: widzisz w jaki sposób chcę to zrobić

Fixed: Też myślałem o tym sposobie Artur, dużo łatwiejszy tylko trzeba na niego wpaść

czupakadabra : na srodek podstawy... czyli muszę policzyć środek odcinka AB a później podstawić odległośc między AB to wysokości h=a√3/2 ?

czupakadabra : hm.... wysokość mam 4√3 środek podstawy (3, 3√3)

Artur_z_miasta_Neptuna: prawie: 1) wyznaczasz wektor [AB] 2) wyznaczasz polowę odcinka AB 3) wyznaczasz wektor prostopadły do wektora [AB] 4) odkładasz od punktu D (środek odcinka) zadaną długość wysokości 'h' po wektorze [DC] który jest prostopadły do [AB] wskazówka −−− będą dwa możliwe polożenia punktu C

czupakadabra : nie wiem za bardzo co co chodzi chyba nie ma sensu żebyś mi tłumaczył .... wyszedł mi [ 4, 4√3 ] ale nawet nie wiem co on oznacza

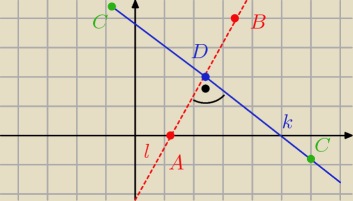
Artur_z_miasta_Neptuna: czupakabra jak nie na wektorach to możesz na prostych ... wektory po prostu troszeczkę szybciej się wyznacza niż proste (jeszcze zależy w jakiej postaci się ów proste chce przedstawić. musisz wyznaczyć prostą prostopadłą do odcinka AB ... przechodząca dokładnie przez połowę tegoż odcinka ... wysokość trójkąta bowiem będzie się zawierać w tej prostej ... a co za tym idzie ... punkt C będzie należeć do tej prostej

Artur_z_miasta_Neptuna: aby wyznaczyć prostą prostopadłą do odcinka AB co musisz mieć albo równanie prostej przechodzącej przez punkty A i B ... albo (wystarczy) wektor [AB] oraz współrzędne środka tegoż odcinka

czupakadabra : prosta przechodząca przez punkt A i B y=√3a ? czyli prostopadła y=i√3/3 ?

czupakadabra : y=−√3/3a więc teraz hm do tej prostej należy punkt D.

Artur_z_miasta_Neptuna: przesunięcie jeszcze ... współczynnik 'b' ... aby D należało

czupakadabra : tylko współczynnik b mi wyszedł 0 ....

Artur_z_miasta_Neptuna:

	√3
i nie y=−		a tylko x
	3

Artur_z_miasta_Neptuna: możliwe ... nie wiem nie sprawdziałem

Artur_z_miasta_Neptuna: nie nie ... 'b' nie może wyjść

	√3
3√3 = −		*3 +b → 3√3 = −√3 + b → b = 4√3
	3

czupakadabra : dla prostej na której leżą A i B mi wyszła √3=a+b 5√3=5a+b −−−−−> a=√3 b=0 fuck

Artur_z_miasta_Neptuna: tam tak ... wychodzi b=0 ale ważniejsze jest 'b' na prostopadlej

Artur_z_miasta_Neptuna: tak jak pisałem ... dla AB wystarczy wektor ... ważna jest prosta prostopadła ... bo ona pokazuje gdzie dokładnie będzie punkt C

czupakadabra : aaaa dalej trzeba od nowa do wzoru y=ab+b podstawiać... tzn dal tej prostopadłej

Artur_z_miasta_Neptuna: dokładnie ... i masz wzór tej prostopadłej na niej szukasz punktu C, który jest oddalony od punktu D o dokładnie 4√3

Artur_z_miasta_Neptuna: i masz współrzędne (dwie możliwości) punktu C koniec zadania

czupakadabra : no ok mam wzór y= √3x+4√3 i wiem że odległośc DC = 4√3

czupakadabra : dla mnie nie koniec bo no mam odległość... mam to podstawić pod wzór na odległośc punktów w układzie współrzędnych ?

Artur_z_miasta_Neptuna: y=√3x + 4√3 D = (3, 3√3) C = (x ; √3x + 4√3) 4√3 = h = √(3−x)² + (3√3−√3x − 4√3)² 16*3 = (3−x)² + 3(x + 1)² i rozwiązujesz

czupakadabra : Dzięki muszę to na spokojnie jeszcze zrobić raz. Jesteś mega

czupakadabra : Kurde jestem totalnie rozkojarzony gdzie Ci uciekły te pierwiastki z drugiego nawiasu że pozostało Ci 3(x+1)²

Artur_z_miasta_Neptuna: (3√3 − √3x − 4√3)² = (−√3 − √3x)² = (−√3)²(1+x)² = 3*(1+x)²

czupakadabra : Idę pod prysznic .... i siadam do tych zadań .... pół godziny będę myśleć nad pomysłem i dopiero zacznę robić ...

Artur_z_miasta_Neptuna: można to też zrobić tylko na wektorach: [AB] = [5−1 ; 5√3 − √3] = [4;4√3] wektor prostopadły do wektora [AB] to: [DD'] = [−4√3,4] (lub [4√3,−4]) długość tego wektora to √16*3+16 = √16*4 = 8

	−4√3		4		−√3		1
tworzę wektor jednostkowy e = [		;		] = [		;		] .. jedno długość
	8		8		2		2

wynosi 1 wysokość trójkąta to 4√3 ... więc chcę utworzyć wektor E równoległy do e ... ale o długości 4√3

	−√3		1
E = [		*4√3,		4√3] = [−6;2√3] (lub [6 ; −2√3])
	2		2

chcę, aby wektor E był tworzony przez punkty D i C D = (3,3√3) E = [x_c − 3 , y_c − 3√3] = [−6 ; 2√3] ⇒ x_c = −3 y_c = 5√3 (lub x_c = 9 ; y_c = √3) i nawet bez równania kwadratowe się obeszło

czupakadabra : Niestety na wektorach jeszcze nie potrafię działać

czupakadabra : Artur jeśli jesteś to jeszcze jedna rzecz kilka zadań już mi wyszło ale wróciłem do tego i na samym końcu nie wiem dlaczgo podstawialiśmy do wzoru na funkcję liniową gdzie współczynnik wynosił √3 a nasza prosta prostopadła miała współczynnik √3\3 ?

Artur_z_miasta_Neptuna: prosta przechodząca przez A i B ma współczynnik √3 co wynika z podstawienia punktów ... i nie trzeba chyba tłumaczyć. Warunek na prostopadłość prostych a*a' = −1 ...

	1		√3
√3 * a' = −1 ⇒ a' = −		= −
	√3		3

i stąd masz taki właśnie współczynnik kierunkowy