Analiza Kipic: Troche Analizy nie zaskodzi Mam jutro test ze studium talent i mam pytanie bo tego zadania nie ogarniam moze mi ktos przyblizyc jak to sie robi : Które z podanych funkcji są na? Dlaczego? a) f : R → (0,∞), f(x) = x² ( jeden przyklad , jak ktos mi pomoze go zrobic reszte sprobuje sm ogarnac) Prosze o wyjasnienie jak to robic bo generalnie wiem co to na ale nie umiem tego wykorzystac Z góry dziekuje

Artur_z_miasta_Neptuna: pytanie za 100pkt ... czy wiesz co to jest funkcja 'na'

Artur_z_miasta_Neptuna: proszę byś mi tu napisał własnymi słowami co to oznacza

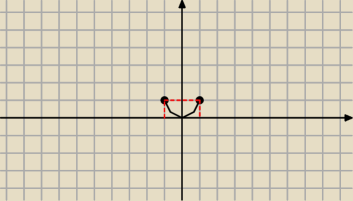
Kipic: wiec wlasnymi slowami to tak ja ogarniam tylko mi sie tu nie smiac ; poprostu gdy mamy np : A−to jest ziór argumentów a B − to jest zbiór wartosci f(a)=b w zbiorze A oznaczam poszczegolne punkty malym a w B male b to f : A−−−>B jest "na" poniewaz funkcja f jest odwzorowaniem zbioru wartosci " na" jesli b∊B i a∊A iumiem robic prste przyklady np f(x) = x² f : [−1;1] to rysuje wiec jest "na" [0;1] wiec to "na" to jest odwzorowanei niewiem czy dobrze ogarniam wiec sie pytam

Kipic: ale juz jak jest z f : R → (0,∞) to nie umiem

Artur_z_miasta_Neptuna: a tam nie ma przypadkiem f:R −> <0;∞)

Artur_z_miasta_Neptuna: a tak na chłopski rozmów −−− funkcja przyjmuje KAŻDĄ wartość ze zbioru B

Kipic: jest f : R → (0,∞)

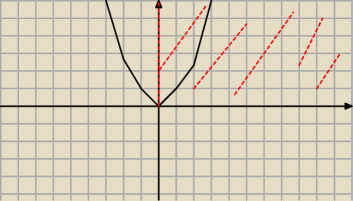
Kipic: to rysunek tak chyba wyglada ale czy ona jest na skoro jedna strona jest bez

Artur_z_miasta_Neptuna: jedna stron jest bez nie bardzo rozumiem. funkcja jest 'na' gdy każdy element zbioru B jest przyjmowany przez odwzorowanie jakiegoś elementu ze zbioru A na kwantyfikatorach: ∀_y∊B ∃_x∊A f(x) = y jak wykazać, że f:R−> (0,∞) ; f(x) = x² jest 'na' najprościej poprzez wykazanie, że: 1) jest to funkcja rosnąca na przedziale (0,∞) 2) jest to funkcja ciągła na tym właśnie przedziale 3) f(0) = 0 z tego wynika ... że funkcja f(x) = x² przyjmuje każdą wartość ze zbioru B=(0,∞)

Kipic: kwalifikatorow nie mialem na wukladach wiec o nich nic nie wiem ale reszte rozumiem dzieki i jak tak bede pisac np slownie to tez bedzie dobrze i zalicza mi ?