Funkcja z wartością bezwzględną Grześ: Witam. Mam takie zadanko do rozwiązania, a jest dla mnie za trudne. Nie wiem od czego zacząć, bo nie rozumiem wartości bezwzględnych. Dana jest funkcja f(x)=|¹₂x+2|+|³₂x−3|−5 a) Napisz wzór funkcji bez użycia symbolu wartości bezwzględnej. b) Narysuj wykres funkcji f. c) Podaj zbiór wartości funkcji g(x)=|f(x)|−3. d) Zapisz wzór funkcji h(x)= ^|f(x)|_f(x) bez użycia symbolu wartości bezwzględnej i narysuj jej wykres. Wiem, że dużo, ale może ktoś rozwiążę W nagrodę cukierek. Pozdrawiam.

Artur_z_miasta_Neptuna: więc zacznijmy od podstaw: def:

	⎧	x ; gdy x≥0
|x| =	⎩	−x ; gdy x<0

innymi słowy |x| to liczba ≥0 gdy wartość pod wyrażeniem jest dodatnia to |x| = x <−−− dodatnia = dodatniej gdy wartość pod wyrazeniem jest ujemna to |x| = −x <−−− dodatnia = − ujemna czyli dodatnia rozumiemy jak na razie

Grześ: No niby tak, ale skąd mam wiedzieć, że w pierwszym przypadku tego zadania pod wartością będzie liczba dodatnia. Nie wiem jakie jest x, więc nie wiem jak opuścić wartość.

Aga1.: Np. To co jest pod wartością bezwzględną przyrównaj do 0 i rozwiąż dwa równania. Rozwiązania zaznacz na osi liczbowej i rozpatruj w trzech przedziałach.

Aga1.:

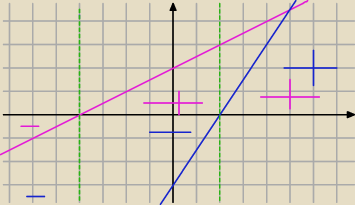
	1
y=		x+2 −−−kolor różowy
	2

	3
y=		x−3 −−kolor niebieski
	2

1) Gdy x<−4, to I1/2x+2I=−1/2x−2 I3/2x−3I=−3/2x+3 2) x∊<−4,2) I1/2x+2I=1/2x+2 I3/2x−3I=−3/2x+3 3) gdy x≥2 I1/2x+2I=1/2x+2 I3/2x−3I=3/2x−3.

Mila:

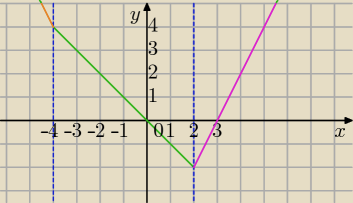
	1		3
f(x)=|		x+2|+|		x−3|−5
	2		2

Artur dał wskazówkę, abyś zbadał.

	1		1
1)		x+2≥0⇔		x≥−2⇔x≥−4
	2		2

	1		1
|		x+2|=		x+2 dla x≥−4
	2		2

	3		3
2)		x−3≥0⇔		x≥3⇔x≥2
	2		2

x<−4

	1		1
|		x+2|=−		x−2
	2		2

	3		3
|		x−3|=−		x+3
	2		2

	1		3
f(x)=−		x−2+(−		x)+3−5⇔f(x)=−2x−4
	2		2

x∊<−4,2)

	1		3
f(x)=		x+2−		x+3−5⇔f(x)=−x
	2		2

x≥2

	1		3
f(x)=		x+2+		x−3−5⇔f(x)=2x−6
	2		2

Grześ: Dzięki wszystkim za podpowiedzi, już rozumiem. Do podpunktu c wszystko czaję. Tam wyjdzie Zw: x≥−3. Tylko nie wiem co mam zrobić z podpunktem d. Niby coś tam kombinuję tak samo w kilku przypadkach, ale jak zapisać ten wzór funkcji? W sensie widzę o co chodzi, ale nie potrafię zapisać, żeby dostać prawidłowe punkty.

Grześ: No i jak wykres narysować.

Artur_z_miasta_Neptuna: zauważ,że: jeżeli f(x) >0 to |f(x)| = f(x)

	|f(x)|
więc		= 1
	f(x)

jeżeli f(x) = 0 to

|f(x)|
	nie istnieje (mianownik nie może być =0)
f(x)

jeżeli f(x) <0 to |f(x)| = −f(x)

	|f(x)|
więc		= −1
	f(x)

i koniec

Grześ: Dzięki za pomoc! Dla wszystkich cukierki: http://nanc.pl/sites/default/files/imagecache/nivo-slider/cukiereki.jpg