| √s3 | ||
( ODP : | √6sinα(3−4sin2α) tam jest 3 potęgi ) | |
| 27 |
... a matura już niebawem ...
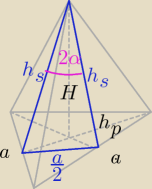dane:
S − pole pow bocznej
2α − kąt
oznaczenia:
a − krawędź podstawy
hp − wysokość podstawy
hs − wysokość ściany
Pp − pole podstawy
H − wysokość ostrosłupa
V − objętość
| 3 | ||
S = | a*hs | |
| 2 |
| 2S | ||
hs = | ||
| 3a |
| a2 | |
= 2hs2 − 2hs2cos2α |*4 | |
| 4 |
| 4S2 | 4S2 | |||
a2 = 8( | ) − 8( | )cos2α |*9a2 | ||
| 9a2 | 9a2 |
| 64 | ||
a4 = | S2sin2α | |
| 9 |
| 8 | ||
a2 = | Ssinα | |
| 3 |
| √8 | √8*√3*√Ssinα | √24*√Ssinα | ||||
a = | *√Ssinα = | = | = | |||
| √3 | 3 | 3 |
| 2√6*√Ssinα | 2 | |||
= | √6S*sinα | |||
| 3 | 3 |
| a√3 | 23√6Ssinα√3 | 2√18Ssinα | √18Ssinα | |||||
hp = | = | = | = | = | ||||
| 2 | 2 | 6 | 3 |
| 3√2Ssinα | ||
= √2Ssinα | ||
| 3 |
| 2S | 2S | S | S√6Ssinα | |||||
hs = | = | = | = | |||||
| 3a | 323√6Ssinα | √6Ssinα | 6S*sinα |
| √6Ssinα | ||
hs = | ||
| 6*sinα |
| 6Ssinα | S | |||
hs2 = | = | |||
| 36sin2α | 6sinα |
| hp | 2Ssinα | |||
( | )2 = | |||
| 3 | 9 |
| S | 2Ssinα | 3S − 4Ssin2α | S(3−4sin2α) | |||||
H2 = | − | = | = | |||||
| 6sinα | 9 | 18sinα | 18sinα |
| √S(3−4sin2α) | √18Ssinα(3−4sin2α) | |||
H = | = | = | ||
| √18sinα | 18sinα |
| 3√2Ssinα(3−4sin2α) | ||
= | ||
| 18sinα |
| √2Ssinα(3−4sin2α) | ||
H = | ||
| 6sinα |
| a2√3 | 83Ssinα√3 | 2 | ||||
Pp = | = | = | √3Ssinα | |||
| 4 | 4 | 3 |
| Pp*H |
| ||||||||||||
V = | = | = | |||||||||||
| 3 | 3 |
| S√3√2Ssinα(3−4sin2α) | √S√S√S√6sin(3−4sin2α) | |||
= | = | |||
| 27 | 27 |