ciagi phil: Dany jest ciąg o wzorze ogólnym: an=^{1+3+5+...+(2n+1)}_n+2−n a) oblicz wyraz ciągu (an) b) zbadaj monotoniczność ciągu (an)

phil: Ktokolwiek dalby rade to rozwiązać?

ICSP: ale nie ma co rozwiązywać Przecież a_n jest podane w zdaniu więc nie ma sensu go obliczać

phil: Sorka miało być oblicz 98 wyraz ciągu an

ICSP: no to najpierw policzę : 1 + 3 + 5 + ... (2n−1) . Co wiem : a₁ = 1 r= 2 a_k = 2n−1. Podstawiając do wzoru na sumę :

1 + 2n − 1
	* n = n2.
2

zatem wracając do a_n

	n2		n2 − n2 − 2n		−2n
an =		− n =		=
	n+2		n+2		n+2

Powinieneś już sobie teraz poradzić

phil: Te 2n−1 ma być? Bo we wzorze w zadaniu mamy 2n+1

phil:

Mila: 1) Należy obliczyć sumę: S=1+3+5 +....+(2n+1) a₁=1 a_k=2n+1, r=2 ustalamy ile jest wyrazów w tej sumie a_k=a₁+(k−1)*r⇔2n+1=1+(k−1)*2⇔k=n+1 liczba wyrazów

	1+2n+1
Sn+1=		*(n+1)
	2

S_n+1=(n+1)²=n²+2n+1

	n2+2n+1
an=		−n
	n+2

	n2+2n+1−n(n+2)
an=
	n+2

	1
an=		, an>0 dla n∊N+
	n+2

	1
an+1=
	n+3

Monotoniczność: I sposób

	1
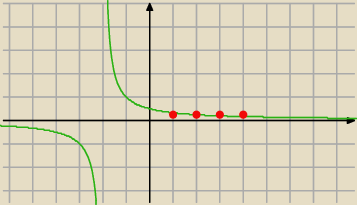
Możesz narysować wykres f(x)=
	x+2

Funkcja malejąca dla x>0, wartości f(n) maleją dla dla n∊N₊ II sposób: badamy iloraz

an+1		1		n+2
	=		*(n+2}=		<1⇔ciąg jest malejący
an		n+3		n+3

	1
a98=
	100