Matura Kipic: Okrąg O₁ o środku w punkcie (4;−2) jest styczny do osi OY . Okrag ten przekształcono przez

	3
jednokładność o skali k = −		i środku w punkcie P nazelzacym do prostej x+2y=0 . Wten
	2

sposób otrzymano okrąg O₂. Podaj równanied okregu o₂ jeśli : a) jest on styczny do osi OY b) jest on styczny do osi OX Wiem że promień to 3 ale dalej robie to na około Co po kolei liczyć Z góry bardzo dziekuje za pomoc

Fixed: http://forum.zadania.info/viewtopic.php?f=29&t=37855 Masz podobne.

Kipic: nie ogarniam

Artur_z_miasta_Neptuna: a czego konkretnie nie ogarniasz

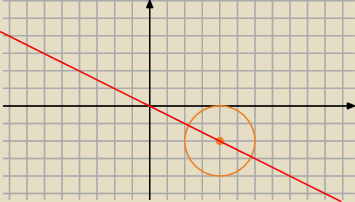
Artur_z_miasta_Neptuna: krok 1) okrąg jest w punkcie (4,−2) i jest styczny do osi OY ... wniosek ... r=2 rysujesz ten okrąg krok 2) rysujesz prostą x+2y=0 krok 3) skoro przekształcono go przez jednokładność o skali k = −3/2 to znaczy, że: przekształcony okrąg będzie większy czy mniejszy od tego narysowanego? będzie on po tej samej stronie czy po drugiej stronie punktu P (który leży 'gdzieś' na tej prostej) ?

Artur_z_miasta_Neptuna: dodatkowo ... jako, że punkt P nie jest dokładnie podany (jest tylko, że jest gdzieś na tej prostej) to będą po dwa rozwiązania do każdego z podpunktów

Fixed: Ale narysowałeś styczny do osi OX

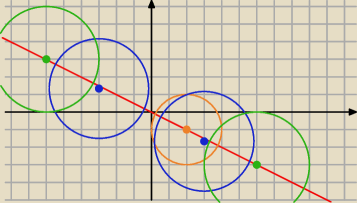
Artur_z_miasta_Neptuna: takie oto będą okręgi

Fixed: No dobra, to chce napisać równanie okręgu O₂ stycznego do osi OY. Z jednokładności obliczam promień, r = 6 Jeżeli styczny do osi OY to współrzędna srodka x = 6 ⋁ x = −6 tak? I teraz wiem ze srodek lezy na prostej x+2y=0 i z tego obliczam wspolrzedne y dla 2 przypadkow, dobrze?

Artur_z_miasta_Neptuna: dokladnie

Fixed: Dzieki, jak sie juz wpadnie na pomysl to zadanie latwiutkie

Artur_z_miasta_Neptuna: tyle że w tym konkretnym zadaniu oczywiście r=3 , żeby nie było

Fixed: r=3?

Artur_z_miasta_Neptuna: startujesz od r=2 jednokładność w skali k=−3/2 nowy promień r_* = 2*(3/2) = 3

Fixed: No ok, ale ten pierwszy okrąg który przekształcamy jest styczny do osi OY to promień nie wynosi |x| ?

Artur_z_miasta_Neptuna: nie rozumiem Ciebie w tym momencie ... promień musi być >0 ... więc musi być |x|

Fixed: No tak, ale Ty podajesz ze r=2, czyli, r=|y|. Tylko, że ten okrąg nie jest styczny do osi OX, tylko OY i wtedy promień to nie jest |x| ?

Artur_z_miasta_Neptuna: jak r=|y| styczny do osi OY więc |x| = r = 2

Artur_z_miasta_Neptuna: cholera ... źle narysowałem

Artur_z_miasta_Neptuna: r = |x| = 4

Artur_z_miasta_Neptuna: znaczy rysunek dobry ...tylko kratka to '2' jednostki a nie '1' i wtedy faktycznie r' = 6

Fixed: Dzieki, o to mi chodzilo

Kipic: Dzieki teraz ja juz tez ogarniam