Wykaż, że podany ciąg jest ograniczony z góry.
wajdzik: Wykaż, że podany ciąg jest ograniczony z góry:
Coś takiego wytworzyłem. Idę dobrym krokiem?
14 mar 22:21
wajdzik: Czy mógłby ktoś pomóc?

14 mar 22:27
wajdzik: 
14 mar 22:31
wajdzik: 
14 mar 22:36
wajdzik: 
14 mar 22:46
wajdzik: 
14 mar 22:52
wajdzik: 
14 mar 23:07
wajdzik: 
14 mar 23:14
oburzona: Nie widzisz, że jest późna pora i myślisz, że ktoś udzieli Ci odpowiedzi. Czekaj cierpliwie do
jutra!
14 mar 23:17
wajdzik: Gdyż ja nie mogę czekać do jutra, wierzę, że ktoś się zlituje i odpowie.

przede mną długa
noc.

14 mar 23:18
jikA:
Funkcja homograficzna teraz jak patrzysz na wykres od n = 1 do ∞ to widzisz że te funkcja jest
malejąca i największa wartość przyjmie w argumencie n = 1.
14 mar 23:25
wajdzik: jikA, nie rozumiem troszkę. Piszesz mi, że największą wartość przyjmie w argumencie n=1.
| | 3n+1 | |
Czy teraz mam do tego: |
| podstawić a1? Jeśli tak to coś tu nie gra, bo 2 |
| | 3n+2 | |
przyjmuje
wartość większą.
14 mar 23:30
asdf: @jika
nie jest malejąca
14 mar 23:40
wajdzik: Wiedziałem, że coś nie gra!

14 mar 23:41
jikA:
| | 2n + 1 | |
Bo ja sobie ubzdurałem że an wygląda |
| |
| | 3n −2 | |
14 mar 23:41
jikA:
| | 2n + 1 | |
Wiadomo że nie jest jeżeli an = |
| robiąc szkic tej funkcji homograficznej |
| | 3n − 2 | |
otrzymasz że ten wykres jest rosnący od n = 1 do
∞.
14 mar 23:43
wajdzik: Późna godzina, dla mnie za późna godzina jak na ciągi. Teraz sobie powtarzam funkcję wymierną.
Ale jeśli będziesz mieć tutaj jakiś pomysł to bardzo poproszę bo CIĄGÓW naprawdę nie
lubię(gdyż ich nie rozumiem). Ale to się zmieni z czasem

14 mar 23:44
jikA:
| | 2n + 1 | | 2 | | k | |
wajdzik zobacz na swój wpis raz piszesz |
| później |
| + |
| . |
| | 3n + 2 | | 3 | | 3n − 2 | |
14 mar 23:45
wajdzik: Czyli a1 jest najmniejszym ogranicznikiem?
14 mar 23:46
jikA:
Stąd wziąłem że ten wykres jest malejący.
14 mar 23:46
wajdzik: Ach te moje roztargnienie. Wybacz.
14 mar 23:47
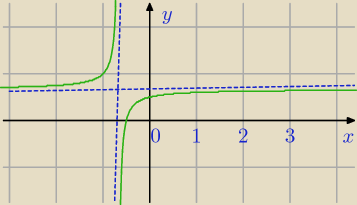
Mila:
==========
| | −2 | |
x= |
| asymptota pionowa |
| | 3 | |
| | 2 | | 2 | |
y= |
| asymptota pozioma ,funkcja rosnąca dla n∊N+ o wartościach< |
| |
| | 3 | | 3 | |
14 mar 23:47
jikA:
Nie wiem zapisz raz a dobrze jak wygląda ta funkcja bo nie chce później sto razy pisać coraz
to inną funkcję.
14 mar 23:47
asdf: | an+1 | | 6n2+ 13n + 6 | | 1 | |
| = |
| = 1 + |
| ..funkcja jest rosnąca |
| an | | 6n2+13n + 5 | | 6n2+13n+5 | |
czyli jak jest rosnąca kla wartości dodatnich, to na bank nie jest ograniczona przez 0.
i teraz dedukcją:
| | 1 | |
2n+1 < 3n + 2 // * |
| (wartosci dodatnie, nie zmienia znaku) |
| | 3n+2 | |
Nie musisz wskazać dokładnej wartości ogarniczającej z góry tylko, wykazać, ze tak jest. Ja tak
bym to zrobil..
14 mar 23:50
wajdzik: Dzięki Mila, a Ciebie jikA przepraszam. Siedzę w tych ciągach cały dzień − może stąd takie
głupie błędy.

14 mar 23:51
wajdzik: Ok, asdf − zapamiętam. Aczkolwiek idę już do łóżka. Sprawdzian z chemii jutro. Tylko jak wrócę
do domu to od razu biorę się dalej za CIĄGI. Dzięki wielkie wszyscy! Dobranoc

14 mar 23:53
jikA:
Nic się nie stało wajdzik skoro jesteś zmęczony to lepiej połóż się już do łóżka i
odpocznij.
14 mar 23:59
Mila: W końcu nie wiem na jakim poziomie mają być te uzasadnienia, LO?
15 mar 00:00
asdf: lub tak jak Mila wskazała − liczysz asymptoty.
| | −5 | |
Pionowa − dla n−>( |
| )+ g = −∞ |
| | 3 | |
ukośna:
a:
b:
| | 2n+3 | | 2 | |
limn−>∞ an − a*n = an − a*0 = limn−>∞ |
| = |
| |
| | 3n+2 | | 3 | |
as. pozioma:
z warunku, że:
| | −5 | | 2 | |
Pionowa − dla n−>( |
| )+ g = −∞ to funkcja rośnie do tej wartości |
| , a jaj nie |
| | 3 | | 3 | |
osiąga jest ograniczeniem z góry.
15 mar 00:01
asdf: @Mila
Masz może jakiś zbiór zadań z szeregu Taylora, szeregu Maclorina? Chodzi o zadania typu:
| | 1 | |
wskaż z dokładnością, np. |
| wartość liczby e..itd. |
| | 10000 | |
15 mar 00:03
jikA:
| | 1 | |
Znaleźć wzór Taylora funkcji f(x) = |
| w punkcie xo = 1. |
| | x | |
15 mar 00:27
vitek1980: @wajdzik
| 2n+1 | | 2n+1 | | 2n+n | |
| < |
| ≤ |
| =1 |
| 3n+2 | | 3n | | 3n | |
czyli ciąg ograniczony z góry
15 mar 10:11
Mila:
Do Asdf, Marku jest trochę zadań jasno rozwiązanych w Krysickim, w I tomie.
Mam stare wydanie.
15 mar 16:35







 przede mną długa
noc.
przede mną długa
noc. 




