Problem z odpowiedzią końcową Alicja: W trójkącie ABC dane są: BC=4cm, AC=2cm, kąt ACB=120. Wyznacz długość odcinka dwusiecznej kata ACB, zawartego w tym trójkącie. Rozwiązałam to zadanie, lecz wyszły mi dwa wyniki x=²₃ oraz x=⁴₃. Poprawny jest tylko x=⁴₃. Dlaczego?

PW: Dwusieczna jest tylko jedna, więc i rozwiązanie może być tylko jedno. Jeżeli ułożone równanie ma dwa pierwiastki, to trzeba się zastanowić, dlaczego jeden z nich nie jest rozwiązaniem "sytuacji geometrycznej". Podaj swoje rozwiązanie, to będzie wiadomo. Stosowałaś dwa razy tw. cosinusów?

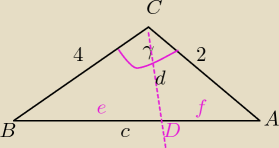
Mila: γ=120⁰ Z tw. cosinusów c²=2²+4²−2*2*4 cos120⁰

	−1
cos1200=cos(180−60)=−cos60=
	2

c²=4+16+8⇔c²=28 c=2√7 z Tw. o dwusiecznej:

4		2
	=
e		f

e+f=2√7

	4√7		2√7
e=		i f=
	3		3

2 razy z tw. cosinusów f²=d²+4−2d e²=d²+16−4d odejmuję stronami f²−e²=−12+2d po podstawieniu za f i e

	4
d=
	3