trapez Kuba: trapez ABCD gdzie AB || CD jest opisany na okregu o promieniu r. Przekątna AC jest nachylona do podstawy AB pod katem α. Oblicz obwód tego trapezu w zaleznosci od kata α i promienia r

Bogdan: Tu kluczową rolę odgrywają rysunki z oznaczeniami. Trójkąty: FSA, ASG, GSB, BSE są przystające. Trójkąty: FSD, DSK, KSC, CSE są przystające.

	y		r		r2
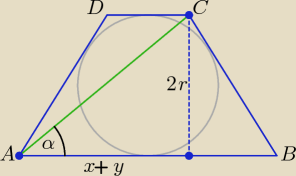
Trójkąty CSE i ESB są podobne, stąd mamy proporcję:		=		⇒ y =
	r		x		x

	4r2
Obwód trapezu: L = 4x + 4y = 4x +
	x

W następnym poście ciąg dalszy, bo potrzebny jest jeszcze jeden rysunek,

Bogdan:

	r2
x + y = x +
	x

	2r		2r		2rx
tgα =		⇒ tgα =		⇒ tgα =
	x + y		r2   x +   x		x2 + r2

2rx = x²tgα + r²tgα (tgα)x² − 2rx + r²tgα = 0

	4r2
Trzeba wyznaczyć z ostatniego równania x i wstawić do wzoru na obwód: L = 4x +
	x

prof. : a nie powinno byc zamiat 4r , 2r

marek mi: tak powinno to wygladac mordy

Bogdan: A gdzie profesorku widzisz zapis 4r ?

Bogdan: Można to zadanie rozwiązać również tak (potrzebne są powyższe 2 rysunki). Obwód L = 4x + 4y (z pierwszego rysunku)

	2r		2r
tgα =		⇒ x + y =		(z drugiego rysunku).
	x + y		tgα

	2r		8r
x + y =		/ *4 ⇒ 4x + 4y =
	tgα		tgα

	8r
Odp.: Obwód L =
	tgα