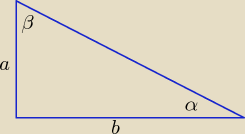
wykaż Kuba: Wykaż , że w trójkacie prostokątnym gdzie α iβ sa kątami ostrymi, to tgα + tgβ ≥ 2

Bogdan: β = 90^o − α tgβ = tg(90^o − α) = ctgα

	sinα		sin2α + cos2α
tgα + ctgα =		+ U{cosα}[sinα} =		=
	cosα		sinα*cosα

	1		2		2		2
=		*		=		=		≥ 2
	sinα*cosα		2		2sinα cosα		sin2α

sin2α ∊ (0, 1>, sin2α może przyjąć maksymalną wartość 1. sin2α = 1 ⇒ α = 45^o. Jeśli α = 45^o, to tgα + tgβ = tgα + ctgα = 1 + 1 = 2.

	2
W każdym innym przypadku tgα + tgβ = tgα + ctgα =		> 2, bo w mianowniku
	sin2α

jest liczba ∊ (0, 1).

Bogdan: Chochlik, poprawiam jeden z zapisów:

	sinα		cosα		sin2α + cos2α		1
tgα + ctgα =		+		=		=
	cosα		sinα		sinα*cosα		sinα*cosα

Kuba: no to ja doszedłem tylko do U {sin²α + cos²α}{sinα*cosα} a póżniej już tak kombinowałem i same bzdury wykombinowałem, ale mam nadzieje że za to jakiś 1 pkt dostane.

Kuba: i tak zrozumiałem chochlika

Eta: Można też tak: tgα= ^a_b ...... tgβ= ^b_a i a² +b² = c² zatem:

	a2 +b2		c2		2ab
tgα+ tgβ= ab + ba =		=		≥		≥2
	ab		ab		ab

ponieważ c² ≥2ab , bo a² +b² ≥2ab => c² ≥2ab

b.: można też niemal bez trygonometrii: podstawmy t=tg α, wtedy tg β = 1/t, i mamy tgα + tgβ = t + 1/t ≥ 2 ze znanej nierówności dla liczb dodatnich t (dowód tej ostatniej: mamy (√t−1/√t)² ≥ 0, skąd t − 2 + 1/t ≥ 0 i ostatecznie t+1/t ≥ 2).

Bogdan: Brawo b.

Eta: ode mnie też