 Wyznacz sklae jdnkladnosci ktora okrag O1 przeksztalca na okrag O2
O1 : x2 + y2 + 2x − 8 = 0
O2 : x2 + y2 −14x−8y + 64 = 0
dobra przeksztalcilem :
O1 : (x+1)2 + y2 =9 czyli O1 =(−1;0) r=3
O1 : (x−7)2+(y−4)=1 czyli O1 =(7,4) r =1
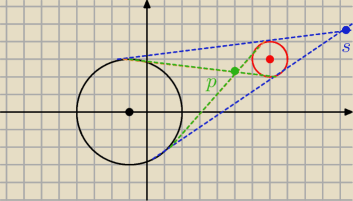
Oczywiscie rysunek nie zaszkodzi i latwo mozna zauwazyc ze sa dwie skale jednokladnosci jedna :
(zielony kolor) k =−3
(niebieski kolor) k=3
no ale to jest słabe
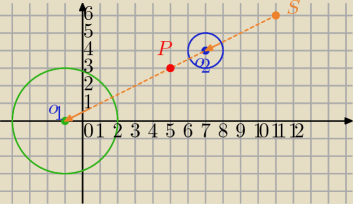
a jak zrobic zeby policzyc algebraicznie srodki P i S oraz skale jednokladnosci obliczyc dla
tych dwoch okregów
Wyznacz sklae jdnkladnosci ktora okrag O1 przeksztalca na okrag O2
O1 : x2 + y2 + 2x − 8 = 0
O2 : x2 + y2 −14x−8y + 64 = 0
dobra przeksztalcilem :
O1 : (x+1)2 + y2 =9 czyli O1 =(−1;0) r=3
O1 : (x−7)2+(y−4)=1 czyli O1 =(7,4) r =1
Oczywiscie rysunek nie zaszkodzi i latwo mozna zauwazyc ze sa dwie skale jednokladnosci jedna :
(zielony kolor) k =−3
(niebieski kolor) k=3
no ale to jest słabe
a jak zrobic zeby policzyc algebraicznie srodki P i S oraz skale jednokladnosci obliczyc dla
tych dwoch okregów 








| 1 | ||
z wektorów |k|= | ||
| 3 |
| 1 | 1 | |||
k*[xs1−xp,ys1−yp]=[xs2−xp,ys2−yp] podstaw pierwsze za k= | a później k=− | |||
| 3 | 3 |

| r2 | 1 | 1 | 1 | |||||
|k|= | = | ⇔k= | lub k=− | |||||
| r1 | 3 | 3 | 3 |
| 1 | ||
1) k= | ||
| 3 |
| 1 | ||
SO2→= | SO1→⇔ | |
| 3 |
| 1 | ||
[7−xs,4−ys]= | *[−1−xs,0−ys] | |
| 3 |
| 1 | 1 | |||
7−xs= | (−1−xs) i 4−ys= | *(−ys) | ||
| 3 | 3 |
| 1 | ||
2)k=− | ||
| 3 |
| 1 | ||
PO2→=− | PO1→⇔ | |
| 3 |
| −1 | −1 | |||
7−xp= | (−1−xp) i 4−yp= | *(−yp) | ||
| 3 | 3 |
