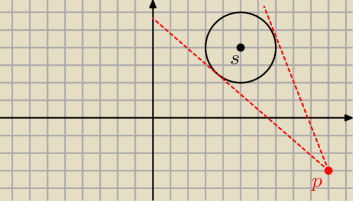
Matura Kipic: Jak najprosciej robic takie zadanie na maturze Dosyc czesto tego typu zadanie sie pojawia Juz kiedys zamieszczalem tego typu zadanie lecz tam odpowiedzi nie byly zbyt oczywiste i na okolo sie zadanie robilo, Moze teraz ktos bedzie wiedziec jak bezproblemowo takie zadanie robic oczywiscie jest podane rownanie okregu czyli (x−5)²+(y−4)²=4 i punkt p ma P(10;−3

Artur_z_miasta_Neptuna: a zadanie tyczy się

Saizou: wyznacz prosta przechodzaca przez punkt P, nastepnie odlegosc tej prostej od srodka okregu jest rowna promieniowi ps. prosta bedzie zalezna od jednej zmiennej

pigor: ... czyżbyś szukał równań stycznych przez dany punkt . ...

Kipic: no wlasnie po raz n−ty wybieglem w przyszlosc oczywiscie tyczy siedo : "napisz rownanie stycznych do okregu"

Kipic: Wiem napewno ze Δ=0 w jakiej postaci zapisac wlasnie ta styczna? ?

Kipic:

Patryk: y=ax+b P(10,−3) −3=10a+b −10a−3=b y=ax−10a−3 (x−5)²+(ax−10a−3−4)²=4 teraz Δ=0

Kipic: no grubo ze tez wczesniej na to nie wpadlem ze z dwoch niewiadomych a i b mozna z punktu P wyliczyc b Dzieks

Patryk: ciesze się ,że mogłem pomóc

Kipic: ja też się cieszę że mi pomogłeś i wszyscy są zadowoleni

Kipic: powiem krotko wychodzi ale obliczenia sa rzeznickie prawie 2 strony hehe ale mozna robic kazde zadanie tego typu automatem no chyba ze punkt P lezy na X lub Y albo jest srodkiem ukladu wspolrzednych wtedy jest jedynie latwo takze bez obliczen duzych zrobic

PW: No, i tu trafiłeś w sedno. Takie zadania najszybciej się rozwiązuje stosując translację o wektor taki, żeby S trafił w środek układu współrzędnych (oczywiście przesuwamy wszystko, nie tylko okrąg). Po wykonaniu łatwiejszych obliczeń "wracamy" stosując translację o wektor przeciwny. Masz u mnie 5.

Mila: Dla Patryka i Kipica || sposób odległość środka okręgu od stycznej jest równa r=2 s: y=ax+b i P∊s P= (10,−3) −3=10a+b⇔b=−10a−3 s: y=ax−10a−3 przekształcam do postaci ogólnej ax−y−10a−3=0 S=(5,4) Korzystam ze wzoru na odległość punktu od prostej

|5a−4−10a−3|
	=2⇔|5a+7|=2√a2+1 /2
√a2+1

25a²+70a+49=4(a²+1)⇔ dokończcie.

Kipic: Mila dobre bo mało obliczeń, wiecej na maturze bedzie czasu na robienie reszty no i przede wszystkim mniejsza szansa na pomyłke .ale tak nick na zólto trochę słabo widoczny teraz jest ledwo przeczytałem już się przyzwyczaiłem do tamtego rózowego