Zakład krawiecki - zad. z prawd. lunnoo: W magazynie są ubrania z trzech zakładów krawieckich X₁, X₂ i X₃. Wiadomo, że z firmy X₁ pochodzi 30% ubrań, z X₂ 50% a z X₃ 20%. Ze względu na jakość produkcja w poszczególnych zakładach kształtuje się następująco: zakład X₁ produkuje 60% ubrań I gatunku, 20% − II gatunku i 20% − III gatunku, zakład X₂ produkuje 40% ubrań I gatunku, 50% − II gatunku i 10% − III gatunku, zakład X₃ produkuje 40% ubrań I gatunku, 40% − II gatunku i 20% − III gatunku. W sposób przypadkowy wzięto ubranie z magazynu. Obliczyć prawdopodobieństwo tego, że pochodzi ono z zakładu X₁, jeśli stwierdzono, ze jest ono pierwszego 1 gatunku.

lunnoo: Bardzo prosiłbym o szczegółowe rozwiązanie (mniej więcej, skąd to się wzięło), gdyż zadanie jest trudne. Podobno trzeba skorzystać ze wzoru Bayesa.

lunnoo: odświeżam

PW: Prawdopodobieństwa zaszyfrowane są w postaci współczynników procentowych. Oznaczmy − żeby już nie wprowadzać następnych oznaczeń − X₁ − wybrana losowo sztuka pochodzi z zakładu X₁ − mamy podane P(X₁)=0,30 X₂ − wybrana losowo sztuka pochodzi z zakładu X₂ − mamy podane P(X₂)=0,50 X₃ − wybrana losowo sztuka pochodzi z zakładu X₃ − mamy podane P(X₃)=0,20 Zdarzenia X₁,X₂,X₃ sa rozłączne parami i suma prawdopodobieństw jest równa 1: 0,30+0,50+0,20=1, spełnione są założenia tw. Bayesa. Niech G₁,G₂,G₃ oznaczają odpowiednio zdarzenia "wylosowano sztukę I gatunku IIgatunku, III gatunku). W zadaniu podano, że P(G₁|X₁)=0,6, P(P(G₂|X₁)=0,2, P(P(G₃|X₁)=0,2, P(G₁|X₂)=0,4, P(P(G₂|X₂)=0,5, P(P(G₃|X₂)=0,1, P(G₁|X₃)=0,4, P(P(G₂|X₃)=0,4, P(P(G₃|X₃)=0,2, P(G₁) policzymy łatwo podstawiając dane do wzoru Bayesa: P(G₁)=P(G₁|X₁)•P(X₁|+P(G₁|X₂)•P(X₂)+P(G₁|X₃)•P(X₃) W zadaniu postawiono pytanie o P(X₁|G₁) − zastosować wzór na prawdopodobieństwo warunkowe.

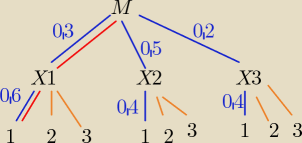
aniabb: P(G1) = 0,3*0,6 + 0,5*0,4 + 0,2*0,4 = ... (niebieskie)

	czerwone		0,3*0,6
P(X1/G1) =		=		= ...
	niebieskie		0,3*0,6 + 0,5*0,4 + 0,2*0,4