matura PuRXUTM: http://www.zadania.info/d1507/76258 mógłby mi ktoś pomóc rozwiązać to pierwsze

Licealista: To z matury z któregoś konkretnego roku, czy próbna?

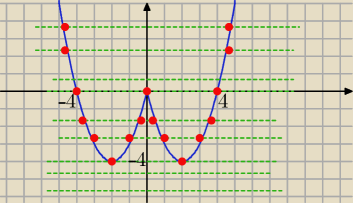Eta: f(x) = x²−4|x| g(x) = −m² 0 rozwiązań dla −m²<0 ⇒ m²>0 ⇒ m€R\{0} 2 " " ............. 3 4

PuRXUTM: szalone zadanie... dlaczego wykres g(x) wygląda tak jak wygląda ? możesz napisać resztę rozwiązań, bo jak by było g(x)=m to bym wiedział a tutaj...

PuRXUTM: @Licealista − to zestaw maturalny z zadania.info

Licealista: Chyba zmienię nick bo jestem w 1lo i każdy się czepia że jak licealista to z 3 klasy...

jikA: Rozwiązanie algebraiczne może być ciekawe.

Eta: 2 rozwiązania dla −m²=−4 v −m² >0 (m−2)(m+2)=0 v m€∅ m=2 v m= −2 3 rozwiązania −m²=0 ⇒ m=0 4 rozwiązania −4< −m²<0 ⇒ ........... dokończ

PuRXUTM: ja się nie czepiam po prostu napisałem

Eta: Pytają o "liczbę rozwiązań" .... więc ja wolę metodę graficzną

PuRXUTM: dzięki Eta takiego zadania jeszcze nie robiłem

Fixed: A jak ma wyglądać ten wykres y= −m² ?

jikA: Wiem Eta tylko napisałem że było by ciekawe ale oczywiście najlepszy i najszybszy sposób pokazałaś.

Eta: y= −m² −−− funkcja stała ( wykresem proste ∥ osi OX

Basia: y + 4|x| = x² y+m² = 0 z (2) y= −m² −m² + 4|x| = x² x² − 4|x| + m² = 0 |x|² − 4|x| + m² = 0 t = |x| t² − 4t + m² = 0 nie ma rozwiązania gdy Δ<0 lub (Δ=0 i t₀<0) lub (Δ>0 i t₁<0 i t₂<0) jedno rozwiązanie gdy ( Δ=0 i t₀≥0) lub (Δ>0 i jeden z pierwiastków jest <0, a drugi ≥0 ) dwa rozwiązania gdy Δ>0 i t₁≥0 i t₂≥0 czy to Ci wystarczy ?

Basia: oj błąd mi się tam wkradł; poprawię

Eta:

jikA: Basia brak rozwiązań można było zapisać dla (Δ < 0) ∨ (Δ ≥ 0 ∧ t₁t₂ > 0 ∧ t₁ + t₂ < 0).

Basia: nie ma rozwiązania gdy Δ<0 lub (Δ=0 i t0<0) lub (Δ>0 i t1<0 i t2<0) jedno rozwiązanie gdy (Δ=0 i t₀=0) lub (Δ>0 i t₁<0 i t₂=0) (nie zachodzi, ale jak ktoś chce algebraicznie musi to rozważyć) dwa rozwiązania gdy (Δ=0 i t₀>0) lub (Δ=0 i t₁<0 i t₂>0) trzy rozwiązania gdy Δ>0 i t₁=0 i t₂>0 cztery rozwiązania gdy Δ>0 i t₁>0 i t₂>0 strasznie dużo liczenia; metoda graficzna jest o wiele szybsza

Basia: [P[⇒jikA] to tylko szkic miał być dalej warunki ma sobie rozpisać osoba zainteresowana rozwiązaniem algenraicznym

PuRXUTM: Basia dziękuje

jikA: Jasne ale algebraicznie napisałaś więc dla Ciebie. Mamy nadzieję PuRXUTM że wiesz o tym x² = |x|² stąd jeżeli Basia podstawiła |x| = t to x² = |x|² = t².

PuRXUTM: a możecie się wypowiedzieć na temat tego 8:2(1+3)=... ?

Eta: 8: 2*4 = 16 ( działana ...od lewej do prawej

Basia: zgodnie z tym co piszą i wmawiają teraz dzieciakom w podstawówce to jest 8:2*4 = 4*4 czyli 16 bo dzielenie i mnożenie są równoprawne i wykonujemy w kolejności zapisu dla mnie ten zapis jest po prostu nie do przyjęcia, bo nie jest jednoznaczny czy zapis (8:2)(1+3) coś komuś utrudnia ? chyba nie, a jest jednoznaczny

PuRXUTM: dzięki tak myślałem, ale ludzie różne rzeczy piszą np. na facebooku jakiś profil związany z matematyką dodał takie zadanie i pod tym w komentarzach "Zatem mamy 4 odpowiedzi 1i 4 odpowiedzi 16, dalej szukamy prawdy " to nie wiem czy chodzi im że jest inne rozwiązanie ( te 4 odpowiedzi czyli 4 posty)

Eta: Hej Basia Tak teraz liczą po wejściu do Unii

PuRXUTM: tak jak 0 nie jest liczbą naturalną po wejściu do Unii

Basia: wiem Eto, ale z uporem maniaka twierdzę, że baran to wymyślił

Eta: ....czytaj <ananas> po wejściu do Unii

PuRXUTM: Basia mogę Twoją wypowiedź zacytować w poście na facebooku ?

Eta: Basiu ja też tak uważam i kiedyś sprzeczałam się,że to nie jest prawdą ( tzn. ten wynik)

PuRXUTM: Drodzy mato fani, znaczenie w tym przykładzie ma prawda, jak widzicie wielu z Was podaje wynik jako prawidłowy 16, inny zaś podają, że jest to 1. Możecie się teraz zastanowić czy naprawdę. W działaniu tym mamy do czynienia ze znakiem, który jest symbolem nieokreślonym i nie możemy wyznaczyć jednoznacznie prawidłowego wyniku a działanie to określamy mianem niejednoznacznego. Kolejność działań w tym przykładzie nie jest możliwa do ustalenia. Jeśli między 2 a nawisam zapisany byłby znak mnożenia to: Odnosząc się do źródeł (Zbigniew Semadeni, „O kolejności wykonywania działań równorzędnych” W: Nauczanie matematyki [on−line]. 6/2007. [dostęp 25 czerwca 2008]) w takich działaniach równorzędnych z dzieleniem i mnożeniem (bez nawiasów), nie ma jednoznacznej, niekwestionowanej umownej reguły postępowania, że działanie to wykonujemy od lewej do prawej strony. „W praktyce na zaawansowanym poziomie nie używa się znaku dzielenia :, lecz stosuje się zapis ułamkowy o dobrze znanych i ściśle określonych regułach. Kwestii kolejności działań w sytuacji mnożenia i dzielenia (bez nawiasów) nie należy definitywnie rozstrzygać poprzez podanie jakiejś jednej ogólnej reguły, która miałaby obejmować wszystkie możliwe przypadki i była zarazem zgodna z praktyką zapisu w publikacjach matematycznych”. Tak napisał ten gościu co to wrzucił na facebooka Basia miałaś rację

Mila: Cała szkolna matematyka jest psuta od lat 70−tych.Wygórowane ambicje(....) i trudny materiał w LO spowodowały, że zrezygnowano z matematyki na maturze i to są straty nie do odrobienia. Nie piszę, o skandalicznych podręcznikach do szkoły podstawowej w latach 80−tych. Reforma i gimnazja − straty nie do odrobienia.