C agh: krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość 4√3cm. Kula wpisana w ten ostrosłup ma promien rowny 2cm. Wyznacz kąt nachylenia ściany bocznej do podstawy tego ostrosłupa oraz oblicz jego objętość.

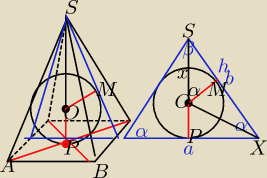
Basia: P punkt przecięcia przekątnych a koło wielkie jest wpisane w ten niebieski trójkąt (nie umiem tego ładnie narysować) a = 4√3 β = 180−2α ΔXMO jest przystający do ΔXPO ⇒ XM = 2√3 ΔSPX ~ ΔSMO (kąty: β/2; 90; α)

SP		SX		PX
	=		=
SM		SO		MO

x+2		hb		2√3
	=		=		= √3
SM		x		2

SM + 2√3 = h_b h_b = √3x SM = √3x − 2√3

x+2
	= √3
√3x−2√3

x+2 = 3x − 6 8 = 2x x=4 h_b = 4√3 zatem niebieski trójkąt jest równoboczny i szukany kąt α=60

	a√3		4√3*√3
zatem H =		=		= 6
	2		2

objętość to już nie problem

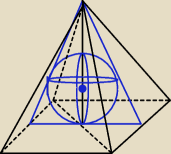Basia: tak to mniej więcej wygląda