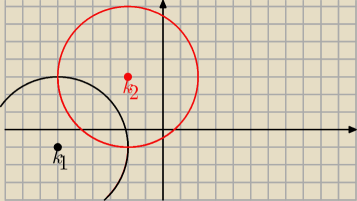
 Kolo K1 : x2 + y2+12x + 2y+21 ≤0 przesuwamy o wektor u=[4;4] i otrzymujemy kolo K2. Oblicz
pole czesi wspolnej tych kół.
Więc :
K1
(x+6)2+(y+1)2≤16
i K2
(x+2)2+(y−3)2≤16
i jak obliczyc te czesc wspolna na necie widzialem wiele roznych odpowiedzi ale tam licozno
chyba nie to co trzeab i oddalano sie od tego co chce sie liczyc zeby dostac odpowiedz
Czy tutaj mozna jakos te dwa rownania do siebie podlozyc i wyznaczyc czesc wspolan poprzez pole
Kolo K1 : x2 + y2+12x + 2y+21 ≤0 przesuwamy o wektor u=[4;4] i otrzymujemy kolo K2. Oblicz
pole czesi wspolnej tych kół.
Więc :
K1
(x+6)2+(y+1)2≤16
i K2
(x+2)2+(y−3)2≤16
i jak obliczyc te czesc wspolna na necie widzialem wiele roznych odpowiedzi ale tam licozno
chyba nie to co trzeab i oddalano sie od tego co chce sie liczyc zeby dostac odpowiedz
Czy tutaj mozna jakos te dwa rownania do siebie podlozyc i wyznaczyc czesc wspolan poprzez pole



| −8−4 | ||
x1= | =−6 i x2=−2 | |
| 2 |
| 1 | 1 | |||
Psoczewki=2*{ | π*42− | 6*6) | ||
| 4 | 2 |