zadania kula
agh: 1)oblicz promien kuli wpisanej w walec,ktorego przekroj osiowy jest kwadratem o przekątnej
długości √2
2)krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość 4√3cm. Kula wpisana w ten
ostrosłup ma promien rowny 2cm. Wyznacz kąt nachylenia ściany bocznej do podstawy tego
ostrosłupa oraz oblicz jego objętość.
13 mar 16:39
dero2005:
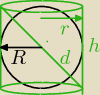
d =
√2
13 mar 17:04
agh: DZIĘKI A WIE KTOS JAK TO 2 ZROBIC?
13 mar 17:24
dero2005:
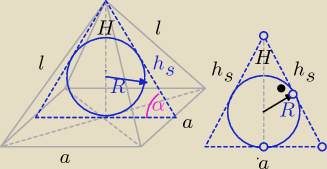
R = 2
a = 4
√3
| a2 | | hs−a2 | |
| = |
| →podobienstwo trójkątów |
| H | | H−R | |
| | R | |
a2*H = |
| (a+2hs) → porównanie pól |
| | 2 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
H>2R
H = 3+
√5
h
s =
√3 +
√15
| | √75 + 2√15 − 3√3 | |
sinα = |
| ≈ 0,93 |
| | 12 | |
sprawdź obliczenia
13 mar 17:43
13 mar 17:43
dero2005:
nie jestem pewien poprawności tych wypocin

13 mar 17:53
agh: OK. DZIĘKUJE

13 mar 18:07
dero2005:
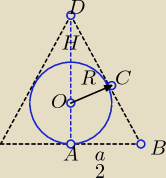
AD = H
AB = BC =
a2 = 2
√3
BD = h
s
OC = AO = R = 2
OD = H − R
| H | | hs−a2 | |
| = |
| → podobieństwo trójkatów |
| hs | | H−R | |
dalej jw.
13 mar 18:18
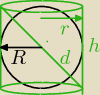 d = √2
d = √2
 R = 2
a = 4√3
R = 2
a = 4√3


 AD = H
AB = BC = a2 = 2√3
BD = hs
OC = AO = R = 2
OD = H − R
AD = H
AB = BC = a2 = 2√3
BD = hs
OC = AO = R = 2
OD = H − R