Zadanie maturalne - wierzchołki równoległoboku Kuczek: Dane są równania prostych zawierających dwa boki równoległoboku 8x + 3y + 1 = 0 i 2x + y −1 = 0 oraz równanie prostej 3x + 2y + 3 = 0 zawierającej jego przekątną. Oblicz współrzędne wierzchołków tego równoległoboku.

Artur_z_miasta_Neptuna: kurdę ... dajesz tutaj juz chyba 10 zadanie ... masz jakiś warunek z matematyki czy po prostu książkę z zadaniami rozwiązać mamy za Ciebie

Artur_z_miasta_Neptuna: masz dwie proste zawierające boki ... ich przecięcie −−− masz już współrzędne jednego boku znając życie ... trzecia prosta zawierająca przekątną ... będzie przecinała wspomniane dwie proste w dwóch różnych punktach −> masz kolejne dwa punkty tego równoległoboku teraz wystarczy już tylko wyznaczyć czwartą współrzędną ... przy wykorzystaniu np. wektorów (np. szukasz punktu B ... mając A,C,D .... znasz odległość DC, współrzędną A ... zaczepiasz wektor o długości DC w punkcie A i wyznacza on współrzedne punktu B)

Kuczek: dokładniej 5, z czego jedno zdążyłem rozwiązać i nie otrzymałem pomocy, drugie nie wiedziałem jak dokończyć mając już większość, w trzecim nie rozumiałem jednej (okazało się) banalnej rzeczy, a tych ostatnich dwóch rzeczywiście nie wiedziałem jak ruszyć. Mimo wszytsko dziękuję za pomoc. Przygotowuję się do matury, staram się codziennie robić dwa arkusze. Te zadania (jest to zbiór kilku które zostały mi z różnych arkuszy) sprawiły mi trudność więc postanowiłem je wrzucić aby ktoś mi je wytłumaczył

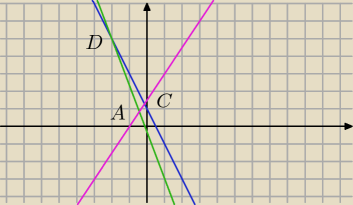
aniabb: brzydkie bo ułamki jeden wierzchołek to D (−2;5)

aniabb: C(−1/7 ; 9/7) A( −11/25 ; 21/25 ) to B ( 28/25 ; −108/25 )