helpppppppppppppppppp
ffffffffff: Mam problem jak obliczyc takie zadanie?Dla jakich wartosci parametru m suma odwrotności dwóch
różnych pierwiastków równania jest równa 6? b)x2−6(m−3)x+m−3=0
12 mar 23:18
Eta:
Parametr "m" spełnia układ warunków:
1/ Δ>0
| | 1 | | 1 | | x1+x2 | |
2/ |
| + |
| = |
| = 6 ( wzory Viete'a |
| | x1 | | x2 | | x1*x2 | |
12 mar 23:21
pomóżcie: a jak obliczyć deltę bo mi nie wychodzi rozwiążesz?

12 mar 23:23
Eta:
Δ= 36(m−3)2−4(m−3) >0 ⇒ 4(m−3)[(9(m−3)−1]>0 ⇒ (m−3)(9m−28)>0
12 mar 23:28
pomóżcie: i co dalej?
12 mar 23:31
Eta:
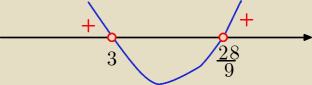
| | 28 | |
1/ Δ>0 ⇔ m€(−∞, 3)U( |
| , ∞) |
| | 9 | |
| | 6(m−3) | |
|
| = 6 , m≠3 ⇒ 6=6 , to m= R\{3} |
| | m−3 | |
| | 28 | |
część wspólna 1/ i 2/ m€(−∞, 3)U{ |
| ,∞) −−− to jest odp. do tego zadania |
| | 9 | |
Dobrej nocy .... leniuchu

12 mar 23:40
Eta:
Zapytam, tak z ciekawości:
czy dostałaś to zadanie do rozwiązania ... kilka minut temu mailem od nauczyciela ?

12 mar 23:44
helpp: nie to jest zadanie domowe a jutro mam z tego kartkowke a jakos mi to nie wychodziłą
12 mar 23:45
helpp: a tak z ciekawości do której klay chodzisz?
12 mar 23:46
Eta:
Do III gimnazjum

12 mar 23:51
helpp: ja do liceum i nie mogłam obliczyć takiego zadania

12 mar 23:52
Eta:

13 mar 00:05






