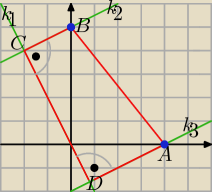
 Prosta k1: y = −2x, a1 = −2.
Prosta k2: y = a2x + b2 jest prostopadła do prostej k1, więc jej współczynnik kierunkowy
Prosta k1: y = −2x, a1 = −2.
Prosta k2: y = a2x + b2 jest prostopadła do prostej k1, więc jej współczynnik kierunkowy
| 1 | ||
a2 = | , prosta ta przechodzi przez punkt B = (0, 5). | |
| 2 |
| 1 | ||
a3 = | , prosta ta przechodzi przez punkt B = (4, 0). | |
| 2 |
 Prosta CD : y= −2x ma współczynnik kierunkowy a = −2
prosta BC jest prostopadła do prostej CD i zawiera punkt B( 0,5)
więc jej równanie jest:
pr. BC: y − yB = −1a*( x − xB)
to: pr. BC: y −5 = 12x => y= 12x +5
podobnie prosta AD jest też prostopadła do prostej CD i zawiera punkt A(4,0)
tO pr. BC: y = 12( x −4) => pr. BC: y = 12x − 2
rozwiązując układy równań:
1/ pr. BC i pr. DC otrzymasz współrzedne punktu C
2/ pr.AD i pr. DC " " " " punktu D
1/ { y = 12x +5
{ y = −2x
2/ { y= 12x − 2
{ y= −2x
to już z pewnością potrafisz
Prosta CD : y= −2x ma współczynnik kierunkowy a = −2
prosta BC jest prostopadła do prostej CD i zawiera punkt B( 0,5)
więc jej równanie jest:
pr. BC: y − yB = −1a*( x − xB)
to: pr. BC: y −5 = 12x => y= 12x +5
podobnie prosta AD jest też prostopadła do prostej CD i zawiera punkt A(4,0)
tO pr. BC: y = 12( x −4) => pr. BC: y = 12x − 2
rozwiązując układy równań:
1/ pr. BC i pr. DC otrzymasz współrzedne punktu C
2/ pr.AD i pr. DC " " " " punktu D
1/ { y = 12x +5
{ y = −2x
2/ { y= 12x − 2
{ y= −2x
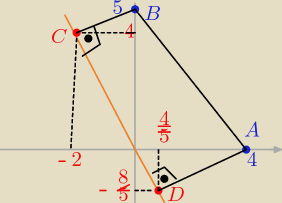
to już z pewnością potrafisz  odp: C( −2, 4) , D( 45, −85) ,
co też potwierdza się na rys. w układzie współrzędnych
odp: C( −2, 4) , D( 45, −85) ,
co też potwierdza się na rys. w układzie współrzędnych