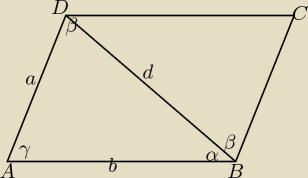
planimetria wikula2013: obicz długosci boków równoległoboku abcd, w którym BD= d, kąt ABD =α, kąt DBC=β

irena_1: Kąt ADB ma miarę β (naprzemianległy z kątem DBC) Kąt ABD ma miarę α Kąt DAB ma więc miarę γ=(180⁰−(α+β)) sinγ=sin(180⁰−(α+β)=sin(α+β) |BD|=d Oznaczyłam: |AD|=a |AB|=b Z twierdzenia sinusów dla trójkąta ABD:

a		d
	=
sinα		sinγ

a		d
	=
sinα		sin(α+β)

	d sinα
a=
	sin(α+β)

Podobnie:

b		d
	=
sinβ		sinγ

b		d
	=
sinβ		sin(α+β)

	d sinβ
b=
	sin(α+β)

irena_1: