Ewa: Wysokość h rombu dzieli jeden z jego boków na odcinki o długosciach 12 i 10 cm oblicz pole rombu i promien okregu wpisanego w ten romb

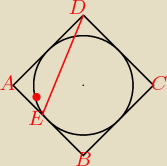
tim: WARIANT I. AE = 10 EB = 12 Korzystając z tych danych i tw. Pitagorasa oblicz h. Znając h łatwo obliczysz pole oraz promień. WARIANT II. AE = 12 EB = 10 AB = AE + EB = ... AB = BC = CD = DA Tak jak wyżej.

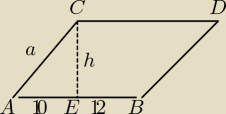AS: AB = a = 10 + 12 = 22 ΔACE: h² + 10² = a² ⇒ h² = 22² − 10² = 484 − 100 = 384 h = √384 = √64*6 = 8*√6 − wysokość rombu Pole rombu: P = a*h = 22*8*√6 = 176*√6 − pole rombu Wysokość romb jest średnicą okręgu wpisanego w romb. 2*r = h

	h
r =		= 8*√6/2 = 4*√6
	2

tim: AS−ie, a druga możliwość?

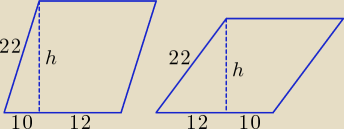Bogdan: Czy jest tylko jedno rozwiązanie?

AS: Niech sama policzy − to jest powtórzenie pierwszego.

tim: Tak, ale dwa warianty. Tak jak napisałem wyżej. Bogdanie − zgadza się.