Rozszerzony planimetria aa: W trójkącie ABC dane są |AC| = 6 , |BC|=10 i kąt ACB = 120 stopni. Wyznacz dł. środkowej CD i długość promienia okręgu opisanego na trójkącie.

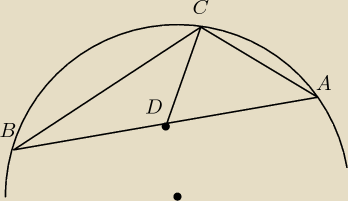
vitek1980: tw. cosinusów dla ΔABC: AB² = 6²+10²−2*6*10*cos120 = 36+100−120*(−0,5) = 136+60 = 196 AB = √196 = 14

	1		1		1
CD =		√2*AC2+2*BC2−AB2 =		√2*36+2*100−196 =		√72+200−196
	2		2		2

	1		1
CD =		√76 =		2√19 = √19
	2		2

chyba

pigor: ..., zaś np. z tw. sinusów : 2Rsin120^o=14 ⇔ 2Rsin60^o=14 ⇔ R√3=14 ⇔ 3R=14√3 ⇔ R= ¹⁴₃√3