??? Abdul: Jak zbadać za pomocą twierdzenia cosinusów czy trójkąt jest prostokątny rozwartokątny lub ostrokątny

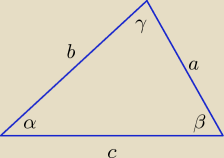
Bogdan: Trzeba wyznaczyć cosinusy kątów z wzoru cosinusów. 1. jeśli wszystkie cosinusy są dodatnie, to trójkąt jest ostrokątny; 2. jeśli jeden z cosinusów jest ujemny, to trójkąt jest rozwartokątny; 3. jeśli jeden z cosinusów jest równy zero, to trójkąt jest prostokątny. Wzory cosinusów:

	−a2 + b2 + c2
a2 = b2 + c2 − 2bc*cosα ⇒ cosα =
	2bc

	a2 − b2 + c2
b2 = a2 + c2 − 2ac*cosβ ⇒ cosβ =
	2ac

	a2 + b2 − c2
c2 = a2 + b2 − 2ab*cosγ ⇒ cosγ =
	2ab

Abdul: Dzięki nie mogłem tego w mojej książce znaleźć

Bogdan: Nie musiało to być w książce. Były natomiast wzory cosinusów, a resztę trzeba samemu ustalić. Tu mamy zwykłe przekształcanie wzorów, wiadomo również, że cos kąta ostrego jest dodatni (I ćwiartka), cos90^o = 0, cos kąta rozwartego jest ujemny (II ćwiartka). Gdyby podręcznik zawierał wszystkie podpowiedzi, to musiałby składać się z kilku opasłych tomów.