okrąg, 2 proste i punkt nowy9555: Witam chciałbym dowiedzieć sie w jaki sposób można obliczyć ( przy podanym równaniu okręgu ) i punkcie wzory obu prostych, które przecinają ten oto punkt i są styczne do okręgu. Byłbym bardzo wdzięczny za rozwiązanie zadania typu równanie okręgu : (x−3)²+(y−6)²=4 punkt przecięcia (7,9) <−−− współrzędne, podaj równania dwóch prostych które przetną punkt i będą styczne do okręgu jest to zadanie z losowymi danymi

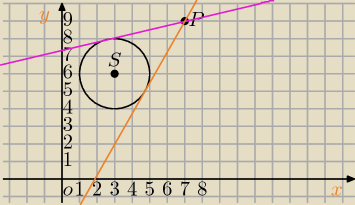
Mila: P=(7,9) S=(3,6) s: y=ax+b i P∊s równanie stycznej 9=7a+b⇔b=9−7a s: y=ax −7a+9 do postaci ogólnej ax−y−7a+9=0 odległość punktu S od prostej s jest równa r=2 U{|3a−6−7a+9|}{√a²+1=2 |3−4a|=2√a²+1 dokończysz, nieładne współczynniki.

nowy9555: Dziękuje