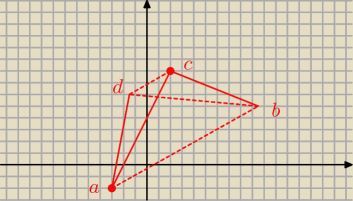
Geometria analityczna Kipic: Hardcorowe zadanie: Dane sa wspolrzedne wierzcholkow A(−3;−2) i C(2;8) trapezu ABCD . OBlicz wspolrzedne punktu przeciecia przekatnych tego trapezu jezeli podstawa AB jest 4 razy dluzsza od podstawy DC wiec walnalem przykladowy rysuneczek : obliczylem ze wektor AB =[5;8] a takze wiem ze : AB = 4DC ale co dalej prosze o wskazowke >><<

Kipic: Juz rozwiazalem

Ann: to się podziel teraz

Kipic: wiec tak robilem mammy znalezc punkt S(x;y) przeciecia dwoch przekatnych i wiemy ze podstawa dolna jest 4 razy dluzsza od gornej wiec: AS = 4 * SC (wektory) [x+3=y+2]=4*[2−x;8−y] x+3=8−4x y+2=32−4y 5x=5 5y=30 x=1 y=6 S(1;6) Tak chyba najp[rosciej zrobic

Mila: AB^→≠[5,8]? AC^→=[5,10] O − punkt przecięcia przekątnych. Napisz jakie wsp. ma punkt O.

	1
AO→=		AC→
	5

Mila: Już widzę. Ładnie.

Kipic:

Lukasz: Jak "działa" wektor na takim przykładzie? Skąd wiadomo że odcinek z wierzchołka do środka to długość 4*odległość środka do przeciwległego wierzchołka?

Lukasz: Już rozumiem

jaros: Własnie ja mam pytanko, skąd on wyliczył wektor AB? i jak rozumiem potem jest jednokłądność, ale z czego wziął tak?

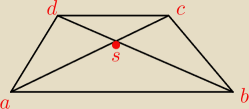
Lukasz: Skoro abs ≈ scd ⇒ AS→=4*SC→ AC→=AS→+SC→ ⇒ AC^→=5SC^→ to wtedy AS^→=⁴₅AC^→ wektor AC = [2+3,8+2] = [5,10] i liczysz wektor AS[a,b] [a,b] = [5*4/5,10*4/5] ⇒ a=4 b=8 AS^→ = [x+3=4 , y+2=8] (x i y punktu S) S=(1,6)