OBLICZ PITER: Zadanie 23 W trojkacie rownoramiennym ABC o podstawie AB poprowadzono wysokosc z wierzcholka C. Wyznacz rownanie prostej zawierajacej te wysokosc, jezeli A = (2,8), B = (−2,4)

rafal: y=0

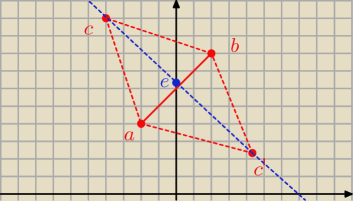
Kipic: Więc robimy przykładowy rysuneczek punkt C moze bycw 2 miejscach wiec oznaczylem C i C' wyznaczamy rownanie kierunkowe przechodzac przez punkty A i B y=ax+b 8=2a+b 4=−2a+b i rozwiazujemy uklad rownan 4=4a a=1 b=6 wiec y =x+6 prosta prostopadla ma: a₁ *a₂ = −1 wiec: y=−1x+b musimy znalezc teraz srodek prostej AB wiec ze wzory na srodek wychodzi punkt E E(0;6) i podstawiamy do prostej prostopadlej y=−1x+b 6=b rownanie prostej prostopadej to y=−x+6