Parametr blan: Wyznacz liczbę rozwiązan równania w zależności od parametru a 1. 3x−1=a+2−ax 2. 2x−a=ax+1 3. Dla jakich wartości parametru m rozwiązaniem równanai |x−1|=m+2 jest para liczb o przeciwnych znakach .

aniabb: 1. (3+a)x = a+3 gdy a≠−3 ma 1 rozwiązanie x=1 gdy a=−3 ma nieskończenie wiele rozwiązań bo 0=0 jest prawdziwe (2−a)x=a+1

	a+1
gdy a≠2 ma 1 rozwiązanie x=
	2−a

gdy a=2 nie ma rozwiązań bo 0=3 jest fałszywe

blan: a dziękuje bardzo

blan: a 3 zad. Jak zrobić algebraicznie ? Bo graficznie fajnie wychodzi ale algebraicznie ?

irena_1: |x−1|=m+2 x−1=m+2 lub x−1=−m−2 x=m+3 lub x=−m−1 (m+3)(−m−1)<0 −(m+3)(m+1)<0 (m+3)(m+1)>0 m∊(−∞; −3) ∪ (−1; ∞)

irena_1: Oczywiście, nie dopisałam założenia: m+2≥0 m≥−2 co daje m ∊(−1; ∞)

Fixed: 1

blan: dziękuje

blan: ale coś nie gra bo w odpowiedzi wychodzi że od (1,+nieskoczoności )

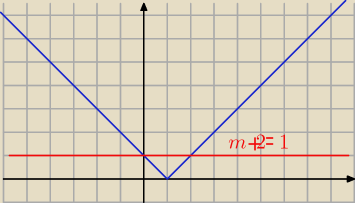
aniabb: więc m> −1 czyli tak jak pisała Irena