Wyznacz obj. ostrosłupa ela: Hej, Mam problem z rozwiązaniem zadania... Ściana boczna ostrosłupa prawidłowego trójkątnego jest trójkątem równoramiennym o wysokości h i kącie przy podstawie α. Wyznacz objętość tego ostrosłupa. dzięki

AROB: Dużo pisania,ale spróbuję.

AROB:

	1		a2√3
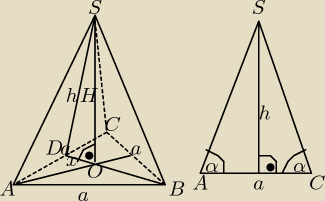
Dane: α, h V = ? V =		*		* H
	3		4

Z trójkąta na ścianie bocznej ACS obliczamy a:

	h		2h
		= tgα , stąd a =
	a/2		tgα

	1
Dla wyznaczenia wysokości H należy obliczyć odcinek x, który jest		wysokości podstawy.
	3

1

a√3

a√3

2h

√3

h√3

x =

*

=

=

*

=

3

2

6

tgα

6

3tgα

H² + x² = h²

	h√3
H2 + (		)2 = h2
	3tgα

	3h2
H2 = h2 −
	9tg2α

	h2
H2 = h2 −
	3tg2α

	3h2tg2α − h2
H2 =
	3tg2α

	h2(3tg2α − 1)
H2 =
	3tg2α

	h√3tg2α − 1		h√3(3tg2α − 1)
Stąd H =		=
	√3tgα		3tgα

	1		√3		2h		h√3(tg2α − 1 )
V =		*		* (		)2 *		=
	3		4		tgα		3tgα

	√3*4h3*√3 *√tg2α − 1
=		=
	36tg3α

	3h3√tg2α − 1		h3√tg2α − 1
=		=
	9tg3α		3tg3α

Mam nadzieję, że się nie pomyliłam (pora niezbyt odpowiednia, ale na narkotyk nie ma rady). Może ktoś rano rzuci okiem.