trapez
dumka: W trapez równoramienny wpisano okrąg o promieniu 4 cm. Ramię trapezu ma długość 10 cm. Punkty
styczności okręgu z ramionami trapezu dzielą obwód trapezu na dwie części. Oblicz stosunek
tych części.
Możecie mi pomóc robie cały czas i nie wychodzi mi nic.
11 mar 21:35
Eta:
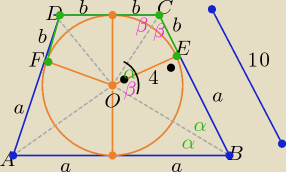
|∡BOC|=90
o ( myślę,że wiesz dlaczego?
|BC|=a+b=10
z podobieństwa trójkątów BOE i COE
| | r | | b | |
|
| = |
| ⇒ r2=a*b ⇒ ab=16 |
| | a | | r | |
rozwiąż układ równań a+b=10 i ab=16 ⇒ a=8 , b=2
| Ob(ECDF) | | 4b | | 1 | |
| = |
| = |
| |
| Ob(ABEF) | | 4a | | 4 | |
11 mar 22:14
dumka: super rysunek, bardzo, ale troche nie wiem czemu tak jest bo przecież nie ma narysowanych
przekątnych, a nie wiem czy te kąty są zgodne w sensie twierdzeń. al ei tak dzieki za
wytłumaczenie może zrozumiem coś
11 mar 22:30
Eta:
Środek okręgu wpisanego w trapez leży w punkcie przecięcia
dwusiecznych kątów
i twierdzenie o odcinkach stycznych
oraz suma katów przy ramieniu jest: 2α+2β= 180
o ⇒α+β=90
o
To trójkąt BOC jest prostokątny o kątach ostrych α i β
Zatem trójkąty BOE i COE są podobne z cechy (kkk)
stąd zależność
r2=a*b
Czy teraz już jasne?

11 mar 22:40
Eta:
A to sprzed 5−ciu lat
Po co je ktoś wyciągnął ?
12 sty 02:00
Andrzej: A co jak trapez jest rombem ?
23 lut 12:51
Eta:
Wtedy stosunek tych części jest równy 1
23 lut 16:10
Tomasz: Dlaczego użyli, że te punkty dzielą obwód na dwie części? Jak to rozumieć
9 mar 21:04
Goblin: Aby skorzystac z twierdzania o rownosci odcinkow stycznych do okregi wyprowadzonych z jednego
punktu lezacego zewnatrz okregu
9 mar 21:27
dyna: δΩ∊
1 mar 20:54
 |∡BOC|=90o ( myślę,że wiesz dlaczego?
|BC|=a+b=10
z podobieństwa trójkątów BOE i COE
|∡BOC|=90o ( myślę,że wiesz dlaczego?
|BC|=a+b=10
z podobieństwa trójkątów BOE i COE
