okrąg wpisany w trójkąt Kence : prosze o pomoc jak to zrobić po kolej w trójkącie prostokątnym krótsza przy prostokątna ma długość 6 a jeden z kątów ma miarę 60stopni . oblicz długość okręgu wpisanego w ten trójkąt

Kence : pomoże ktoś

baklazan: korzystajac z funkcji trygonometrycznych znajdujesz drugi bok lub 2, bo po znalazieniu 1 mozesz skorzystac z twierdzenia pitagorasa, a potem korzystasz ze wzoru na dlugosc promienia wpisanego w trojkat prostokatny

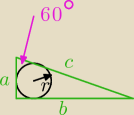
dero2005: a = 6

a		1
	= cos 60o =
c		2

c= 2a = 12 b = √c² − a² = √144 − 36 = √108 = 6√3

	a*b		36√3
P =		=		= 18√3
	2		2

P = ^r₂(a+b+c) = ^r₂(6+6√3+12) = ^r₂(18+6√3) ^r₂(18+6√3) = 18√3 r(18+6√3) = 36√3

	36√3
r =		= 3(√3−1)
	18+6√3

O = 2πr = 6π(√3−1)