tw. sin krzysiek: W trójkącie ostrokątnym ABC tangens kąta przy wierzchołku c jest równy 2 √5 /5, a bok przeciwległy temu kątowi ma długość 12. a) oblicz promień koła opisanego na tym trójkącie b) w trójkącie ABC poprowadzono wysokości AE i BF które przecięły się w punkcie M. Wykaż, że promień okręgu opisanego na trójkącie ABC jest równy promieniowi okręgu opisanego na trójkącie ABM..

Piotruś: Ktoś umiałby zrobić podpunkt b)?

Karlo:

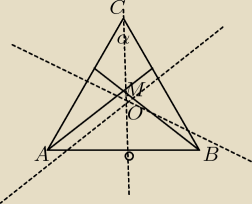
	a		a
Udowodnij to z tw sinusów.		= 2r i zobacz czy		jest tyle samo
	sinα		sinAMB

Piotruś: A czy to można bez kalkulatora i tej tabelki obliczyć? Bo wychodzi mi, że sinα=2/3

Tux: Podbijam, mam ten sam problem